题目内容
17.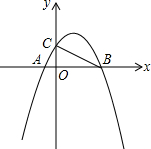 如图,二次函数y=-x2+ax+b的图象与x轴交于$A(-\frac{1}{2},0)$,B(2,0)两点,且与y轴交于点C.
如图,二次函数y=-x2+ax+b的图象与x轴交于$A(-\frac{1}{2},0)$,B(2,0)两点,且与y轴交于点C.(1)求该抛物线的解析式,并判断△ABC的形状;
(2)在此抛物线上是否存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形?若存在,求出P点的坐标;若不存在,说明理由.
分析 (1)由于二次函数y=-x2+ax+b的图象经过$A(-\frac{1}{2},0)$,B(2,0)两点,利用待定系数法就可以直接求出a、b的值,求出抛物线的解析式;
(2)在(1)题已将证得∠ACB=90°,若A、C、B、P四点为顶点的四边形是直角梯形,则有两种情况需要考虑:
①以BC、AP为底,AC为高;可先求出直线BC的解析式,进而可确定直线AP的解析式,联立抛物线的解析式即可求出点P的坐标.
②以AC、BP为底,BC为高;方法同①.
解答 解:(1))∵二次函数y=-x2+ax+b的图象经过$A(-\frac{1}{2},0)$,B(2,0)两点,
由题意,得$\left\{\begin{array}{l}{-\frac{1}{4}-\frac{1}{2}a+b=0}\\{-4+2a+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=1}\end{array}\right.$,
∴抛物线的解析式为:y=-x2+$\frac{3}{2}$x+1,
∴C(0,1),
∴AC2=AO2+CO2=$\frac{5}{4}$,
CB2=BO2+CO2=5,
AB2=$\frac{25}{4}$,
∴AC2+CB2=AB2,
∴△ACB是直角三角形;
(2)存在,点P($\frac{5}{2}$,-$\frac{3}{2}$)或(-$\frac{5}{2}$,-9);
若以A、C、B、P四点为顶点的直角梯形以BC、AP为底;
∵B(2,0),C(0,1),
∴直线BC的解析式为:y=-$\frac{1}{2}$x+1;
设过点A且平行于BC的直线的解析式为y=-$\frac{1}{2}$x+h,
将点A(-$\frac{1}{2}$,0)代入得:(-$\frac{1}{2}$)×(-$\frac{1}{2}$)+h=0,h=-$\frac{1}{4}$;
∴y=-$\frac{1}{2}$x-$\frac{1}{4}$;
联立抛物线的解析式有:
$\left\{\begin{array}{l}{y=-\frac{1}{2}x-\frac{1}{4}}\\{y=-{x}^{2}+\frac{3}{2}x+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{1}{2}}\\{y=0}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=-\frac{3}{2}}\end{array}\right.$.
∴点P($\frac{5}{2}$,-$\frac{3}{2}$),
若以A、C、B、P四点为顶点的直角梯形以AC、BP为底,
同理可求得P(-$\frac{5}{2}$,-9);
故当P($\frac{5}{2}$,-$\frac{3}{2}$)或(-$\frac{5}{2}$,-9)时,以A、C、B、P四点为顶点的四边形是直角梯形.
点评 本题是一道二次函数的综合试题,考查了待定系数法求抛物线的解析式,相似三角形的判定与性质,二次函数与不等式的关系,直角梯形的运用,涉及的知识点较多,难度较大.

| A. |  | B. |  | ||
| C. |  | D. |  |
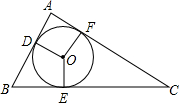 如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )
如图,⊙O是△ABC的内切圆.切点分别为D、E、F,若∠DOE=120°,∠EOF=150°,则△ABC的3个内角的度数依次为( )| A. | 90°,60°,30° | B. | 80°,60°,40° | C. | 90°,50°,40° | D. | 80°,70°,30° |
 如图,AB=AC,∠A=50°,AB的垂直平分线MN交AC于点D,则∠DBC=15°.
如图,AB=AC,∠A=50°,AB的垂直平分线MN交AC于点D,则∠DBC=15°.
 已知如图:AE=DB,∠C=∠F,BC∥EF.求证:AC∥DF.
已知如图:AE=DB,∠C=∠F,BC∥EF.求证:AC∥DF.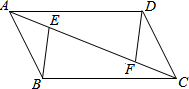 如图,在四边形ABCD中,点E、F在AC上,有下面五个论断:
如图,在四边形ABCD中,点E、F在AC上,有下面五个论断:



 如图,DE∥BC,S△DOE:S△COB=4:9,求AD:BD.
如图,DE∥BC,S△DOE:S△COB=4:9,求AD:BD.