题目内容
4.解不等式组$\left\{\begin{array}{l}{2x-4≤\frac{1+x}{2}}\\{3(2-x)≤x+2}\end{array}\right.$,并将解集在数轴上表示出来.分析 分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.
解答 解:$\left\{\begin{array}{l}2x-4≤\frac{1+x}{2}①\\ 3(2-x)≤x+2②\end{array}\right.$,由①得,x≤3,由②得,x≥1,
所以原不等式组的解集为1≤x≤3.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.一个正多边形形的内角和是1440°,则它的每个外角的度数是( )
| A. | 30° | B. | 36° | C. | 45° | D. | 60° |
19.下列各数是无理数的是( )
| A. | $\sqrt{4}$ | B. | -$\frac{1}{3}$ | C. | π | D. | -$\root{3}{8}$ |
16.一次函数y=(m+2)x+1,若y随x的增大而增大,则m的取值范围是( )
| A. | m>-2 | B. | m>2 | C. | m<-2 | D. | m<2 |
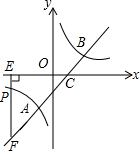 如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(-1,m).
如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(-1,m). 在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm,则OB=$\sqrt{73}$cm.
在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm,则OB=$\sqrt{73}$cm.