题目内容
5.解方程组$\left\{\begin{array}{l}{3x-2y-14=0}\\{4x+3y+4=0}\end{array}\right.$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{3x-2y=14①}\\{4x+3y=-4②}\end{array}\right.$,
①×3+②×2得:17x=34,即x=2,
把x=2代入①得:y=-4,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-4}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
16.一次函数y=(m+2)x+1,若y随x的增大而增大,则m的取值范围是( )
| A. | m>-2 | B. | m>2 | C. | m<-2 | D. | m<2 |
17.下列运算中,正确的是( )
| A. | a2+a=2a3 | B. | a2•a3=a5 | C. | (a2)3=a5 | D. | (ab2)3=a3b2 |
15.不等式$\frac{2x-1}{3}$+2>x的解集是( )
| A. | x<5 | B. | x>-5 | C. | x>-1 | D. | x<1 |
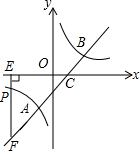 如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(-1,m).
如图,直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,已知点A的坐标为(-1,m). 在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm,则OB=$\sqrt{73}$cm.
在?ABCD中,点O是对角线AC、BD的交点,AC垂直于BC,且AB=10cm,AD=8cm,则OB=$\sqrt{73}$cm.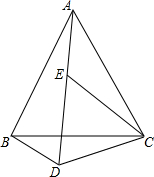 如图,已知点D是等边三角形ABC外的一点,将△BCD绕点C顺时针旋转至△ACE处.
如图,已知点D是等边三角形ABC外的一点,将△BCD绕点C顺时针旋转至△ACE处.