题目内容
 已知,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG,
已知,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG,(1)观察猜想BE与DG之间的大小关系,并证明你的结论;
(2)观察猜想BE与DG之间的位置关系,并证明你的结论;
(3)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程;若不存在,并说明理由.
考点:旋转的性质,正方形的性质
专题:
分析:(1)利用正方形的性质以及全等三角形的判定得出△BCE≌△DCG,进而得出答案;
(2)利用全等三角形的性质得出对应角进而得出答案;
(3)利用旋转的性质得出答案.
(2)利用全等三角形的性质得出对应角进而得出答案;
(3)利用旋转的性质得出答案.
解答: 解:(1)BE=DG,
解:(1)BE=DG,
理由:∵正方形ABCD的边CD在正方形ECGF的边CE上,
∴BC=DC,CG=EC,
在△BCE和△DCG中
,
∴△BCE≌△DCG(SAS),
∴BE=DG;
(2)互相垂直,
理由:延长GD到BE于点N,
∵△BCE≌△DCG,
∴∠BEC=∠CGD,
又∵∠NDE=CDG,
∴∠DCG=∠END=90°,
∴BE与DG之间的位置关系是互相垂直;
(3)通过旋转互相重合的两个三角形得到,
即△DCG绕点C逆时针旋转90°得到.
 解:(1)BE=DG,
解:(1)BE=DG,理由:∵正方形ABCD的边CD在正方形ECGF的边CE上,
∴BC=DC,CG=EC,
在△BCE和△DCG中
|
∴△BCE≌△DCG(SAS),
∴BE=DG;
(2)互相垂直,
理由:延长GD到BE于点N,
∵△BCE≌△DCG,
∴∠BEC=∠CGD,
又∵∠NDE=CDG,
∴∠DCG=∠END=90°,
∴BE与DG之间的位置关系是互相垂直;
(3)通过旋转互相重合的两个三角形得到,
即△DCG绕点C逆时针旋转90°得到.
点评:此题主要考查了全等三角形的判定与性质以及正方形的性质和旋转的性质等知识,得出全等三角形是解题关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若-2x2-1与4x2-4x-5互为相反数,则( )
| A、x=-3或x=1 | ||||||||||||
B、x=1+
| ||||||||||||
| C、x=3或x=-1 | ||||||||||||
D、x=-1+
|
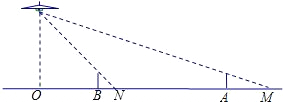 如图,路灯距地面8cm,身高1.6m的小明从距离路灯的底部(点O)20m的点A处,沿AO所在直线行走14m到达B点时,他的影长有多大变化?
如图,路灯距地面8cm,身高1.6m的小明从距离路灯的底部(点O)20m的点A处,沿AO所在直线行走14m到达B点时,他的影长有多大变化?