题目内容
(1)已知:如图1,AB∥CD,求证:∠B+∠D=∠BED;
(2)已知:如图2,AB∥CD,试探求∠B、∠D与∠E之间的数量关系,并说明理由.

(2)已知:如图2,AB∥CD,试探求∠B、∠D与∠E之间的数量关系,并说明理由.

考点:平行线的性质
专题:
分析:(1)根据平行线性质得出∠1=∠B,∠2=∠D,即可得出答案;
(2)根据平行线性质求出∠BEF=∠B,∠DEF=∠CDE,即可得出答案.
(2)根据平行线性质求出∠BEF=∠B,∠DEF=∠CDE,即可得出答案.
解答:(1)证明:如图1,过E点作EF∥AB,
则∠1=∠B,
又∵AB∥CD,
∴EF∥CD,
∴∠B+∠D=∠1+∠2,
即∠BED=∠B+∠D.
(2)解:∠B-∠D=∠E,
理由:如图2,过E点作EF∥AB,
则∠BEF=∠B,
又∵AB∥CD,
∴EF∥CD,
∴∠DEF=∠CDE,
又∵∠BEF-∠DEF=∠BED,
∴∠B-∠CDE=∠BED.

则∠1=∠B,
又∵AB∥CD,
∴EF∥CD,
∴∠B+∠D=∠1+∠2,
即∠BED=∠B+∠D.
(2)解:∠B-∠D=∠E,
理由:如图2,过E点作EF∥AB,
则∠BEF=∠B,
又∵AB∥CD,
∴EF∥CD,
∴∠DEF=∠CDE,
又∵∠BEF-∠DEF=∠BED,
∴∠B-∠CDE=∠BED.
点评:本题考查了平行线性质的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 已知,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG,
已知,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG,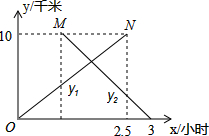 某中学九年级甲、乙凉拌商定举行一次远足活动,A、B两地相距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地.乙班比甲班晚出发一小时.设步行时间为x小时,甲、乙两班离A地的距离分别为y1、y2千米,y1、y2与x的函数关系图象如图所示.根据图象解答下列问题:
某中学九年级甲、乙凉拌商定举行一次远足活动,A、B两地相距10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地.乙班比甲班晚出发一小时.设步行时间为x小时,甲、乙两班离A地的距离分别为y1、y2千米,y1、y2与x的函数关系图象如图所示.根据图象解答下列问题: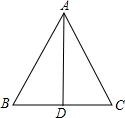 如图,在△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,△ABC是等腰三角形吗?为什么?
如图,在△ABC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,△ABC是等腰三角形吗?为什么?