题目内容
5.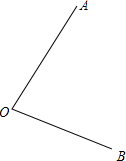 已知∠AOB.
已知∠AOB.(1)用尺规作出∠AOB平分线0D;
(2)画出OB、OD的方向延长线OE、OF;
(3)写出与∠EOF互补的角∠DOE、∠BOF、∠AOF;
(4)若∠AOE=80°,则∠EOF的余角度数为50°.
分析 (1)利用基本作图作OD平分∠AOB;
(2)利用几何语言画出射线OE、OF即可;
(3)∠BOD=∠AOD=∠EOF,然后找出这三个角的邻补角即可;
(4)先利用邻补角计算出∠AOB的度数,再根据角平分线定义计算出∠BOD的度数,然后根据对顶角的性质求∠EOF的度数.
解答 解:(1)如图,OD为所作;
(2)如图,OE、OF为所作;
(3)与∠EOF互补的角有∠DOE、∠BOF、∠AOF;
(4)∵∠AOE=80°,
∴∠AOB=180°-80°=100°,
∵OD平分∠AOB,
∴∠BOD=$\frac{1}{2}$∠AOB=50°,
∴∠EOF=∠BOD=50°.
故答案为∠DOE、∠BOF、∠AOF;50°.
点评 本题考查了基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.

练习册系列答案
相关题目
13.下列计算:①(x+3)(x-3)=x2+(-3)2;②(a-b)2=a2-b2;③(-x-y)2=x2+2xy+y2;④(2x-y)(y-2x)=4x2-y2.其中错误的个数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
20.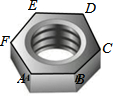 如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
 如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )| A. | $6\sqrt{3}$cm | B. | 12cm | C. | $12\sqrt{3}$cm | D. | 36 cm |
7.若实数x、y满足$\sqrt{x+y-1}$+(y+3)2=0,则x+y的值为( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |
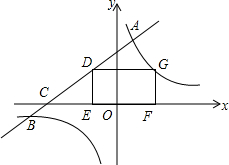 如图,直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=$\frac{3}{2}$,CE=2,点A的横坐标是1.
如图,直线y=kx+b与双曲线y=$\frac{3}{x}$相交于点A,B,与x轴相交于点C,矩形DEFG的端点D在直线AB上,E,F在x轴上,点G在双曲线上,若DE=$\frac{3}{2}$,CE=2,点A的横坐标是1. 如图,已知AD∥BC,∠1=∠2,判断∠BEF与∠DFE的大小关系并说明理由.
如图,已知AD∥BC,∠1=∠2,判断∠BEF与∠DFE的大小关系并说明理由. 已知数轴上数a、b、c对应点的位置如图所示,化简|c-b|+|c-a|-|b-a|.
已知数轴上数a、b、c对应点的位置如图所示,化简|c-b|+|c-a|-|b-a|.