题目内容
20.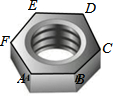 如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )
如图,螺母的一个面的外沿可以看作是正六边形,这个正六边形ABCDEF的半径是$2\sqrt{3}$cm,则这个正六边形的周长是( )| A. | $6\sqrt{3}$cm | B. | 12cm | C. | $12\sqrt{3}$cm | D. | 36 cm |
分析 由正六边形的性质证出△AOB是等边三角形,由等边三角形的性质得出AB=OA,即可得出答案.
解答 解:设正六边形的中心为O, 连接AO,BO,如图所示:
连接AO,BO,如图所示:
∵O是正六边形ABCDEF的中心,
∴AB=BC=CD=DE=EF=FA,∠AOB=60°,AO=BO=2$\sqrt{3}$cm,
∴△AOB是等边三角形,
∴AB=OA=2$\sqrt{3}$cm,
∴正六边形ABCDEF的周长=6AB=12$\sqrt{3}$cm.
故选:C.
点评 此题主要考查了正多边形和圆、等边三角形的判定与性质;根据题意得出△AOB是等边三角形是解题关键.

练习册系列答案
相关题目
11.教材中“整式的加减”一章的知识结构如图所示,则A和B分别代表的是( )


| A. | 分式,因式分解 | B. | 二次根式,合并同类项 | ||
| C. | 多项式,因式分解 | D. | 多项式,合并同类项 |
8.下列计算错误的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\sqrt{6}$÷$\sqrt{2}$=$\sqrt{3}$ | C. | (-$\sqrt{3}$)2=3 | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
12. 实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
 实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )| A. | b | B. | d | C. | a | D. | c |
2.点到直线的距离是( )
| A. | 点到直线的垂线段的长度 | B. | 点到直线的垂线段 | ||
| C. | 点到直线的垂线 | D. | 点到直线上一点的连线 |
 已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F.
已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F. 已知∠AOB.
已知∠AOB. 如图,动点A从原点出发向数轴正方向运动,同时,动点B也从原点出发向数轴负方向运动.已知点A比点B每秒多运动2个单位长度,4秒后两点相距24个单位长度.
如图,动点A从原点出发向数轴正方向运动,同时,动点B也从原点出发向数轴负方向运动.已知点A比点B每秒多运动2个单位长度,4秒后两点相距24个单位长度.