题目内容
11.(1)计算:$\sqrt{12}$+($\sqrt{3}$-1)0-2sin60°+3-1.(2)先化简,后计算:($\frac{81-{a}^{2}}{{a}^{2}+6a+9}$÷$\frac{9-a}{2a+6}$)•$\frac{1}{a+9}$,其中a=$\sqrt{3}$-3.
分析 (1)利用零指数幂,负整数指数幂的法则及特殊角的三角函数值求解即可,
(2)先化简,再把a=$\sqrt{3}$-3代入求值即可.
解答 解:(1)计算:$\sqrt{12}$+($\sqrt{3}$-1)0-2sin60°+3-1
=2$\sqrt{3}$+1-2×$\frac{\sqrt{3}}{2}$+$\frac{1}{3}$,
=$\sqrt{3}$+$\frac{4}{3}$.
(2)($\frac{81-{a}^{2}}{{a}^{2}+6a+9}$÷$\frac{9-a}{2a+6}$)•$\frac{1}{a+9}$
=$\frac{(9-a)(9+a)}{(a+3)^{2}}$×$\frac{2(a+3)}{9-a}$×$\frac{1}{a+9}$,
=$\frac{2}{a+3}$,
当a=$\sqrt{3}$-3时,原式=$\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查了分式的化简求值,解题的关键是熟记零指数幂,负整数指数幂的法则及特殊角的三角函数值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.有一个数阵排列如图:则第20行从左至右第10个数为( )


| A. | 425 | B. | 426 | C. | 427 | D. | 428 |
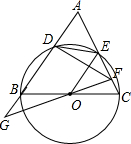 如图,在△ABC中,以BC为直径的⊙O,交AB、AC于点D、E,连接DE.
如图,在△ABC中,以BC为直径的⊙O,交AB、AC于点D、E,连接DE.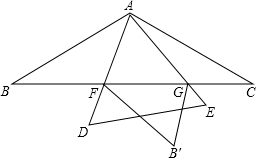 如图,△ABC中,AB=AC=4,∠BAC=120°,以A为一个顶点的等边三角形ADE绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G.若点B关于直线AD的对称点为B′,当△FGB′是以点G为直角顶点的直角三角形时,BF的长为4$\sqrt{3}$-4.
如图,△ABC中,AB=AC=4,∠BAC=120°,以A为一个顶点的等边三角形ADE绕点A在∠BAC内旋转,AD、AE所在的直线与BC边分别交于点F、G.若点B关于直线AD的对称点为B′,当△FGB′是以点G为直角顶点的直角三角形时,BF的长为4$\sqrt{3}$-4.