题目内容
11.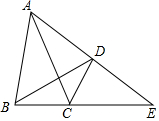 如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.
如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.(1)求证:△ACE∽△BDE;
(2)已知DE=4,CD=3,BE=8,求AB的长.
分析 (1)根据邻补角的定义得到∠BDE=∠ACE,又因为又∠E=∠E,所以可证明△ECA∽△EDB
(2)由相似三角形的性质即可得到结论.
解答 (1)证明:∵∠ADB=∠ACB,
∴∠EDB=∠ECA.
又∠E=∠E,
∴△ECA∽△EDB,
(2)解:∵△ECA∽△EDB
∴$\frac{DE}{EC}$=$\frac{BE}{AE}$,
∴$\frac{DE}{BE}$=$\frac{EC}{AE}$,∵∠E=∠E,
∴△ECD∽△EAB,
∴$\frac{CD}{AB}$=$\frac{ED}{BE}$,
∴$\frac{3}{AB}$=$\frac{4}{8}$,
∴AB=6.
点评 本题考查了相似三角形的判定和性质,邻补角的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2. 如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
 如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )
如图,菱形ABCD中,∠A=60°,AB=6,⊙A、⊙B的半径分别为4和2,P、E、F分别是边CD、⊙A和⊙B上的动点,则PE+PF的最大值是( )| A. | 6$\sqrt{3}$+12 | B. | 6$\sqrt{3}$+16 | C. | 18 | D. | 6 |
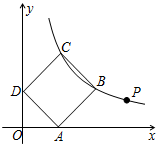 如图,点P(4,1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图,点P(4,1)在双曲线y=$\frac{k}{x}$(x>0)上.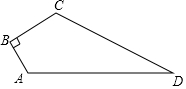 某单位有一块四边形的空地,∠B=90°,量得各边的长度AB=3米,BC=4米,CD=12米,AD=13米,现计划在空地内种草.
某单位有一块四边形的空地,∠B=90°,量得各边的长度AB=3米,BC=4米,CD=12米,AD=13米,现计划在空地内种草.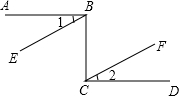 如图,从下列条件中:
如图,从下列条件中: 已知直线AB和直线外一点P,过点P画直线AB的垂线,垂足为O;过点P画直线AB的平行线CD.
已知直线AB和直线外一点P,过点P画直线AB的垂线,垂足为O;过点P画直线AB的平行线CD.