题目内容
6.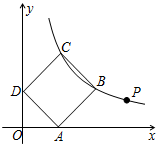 如图,点P(4,1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图,点P(4,1)在双曲线y=$\frac{k}{x}$(x>0)上.(1)则k的值为4;
(2)若正方形ABCD的顶点B,C在双曲线y=$\frac{k}{x}$(x>0)上,顶点A,D分别在x轴和y轴的正半轴上,求点C的坐标.
分析 (1)将点P的坐标代入双曲线解析式中解答即可;
(2)过点B作BE⊥OA于点E,过点C作CF⊥OD于点F,易证得:△DOA≌△AEB≌△CFD,易得B(a+b,a),C(b,a+b),继而求得a的值,则可求得点C的坐标.
解答 解:(1)点P(4,1)在双曲线y=$\frac{k}{x}$上,
将x=4,y=1代入解析式可得:
k=4;
故答案为:4;
(2)过点B作BE⊥OA于点E,过点C作CF⊥OD于点F,
∵四边形ABCD是正方形,
∴AB=AD=DC,∠CDA=90°,
∴∠FDC+∠ODA=90°,
∵∠CFD=∠DOA=90°,
∴∠FCD+∠FDC=90°,
∴∠FDC=∠OAD,
在△CFD和△AOD中,
$\left\{\begin{array}{l}{∠CFD=∠DOA}\\{∠FDC=∠OAD}\\{DC=AD}\end{array}\right.$,
∴△CFD≌△AOD(AAS),
同理可得:△DOA≌△AEB≌△CFD,
∴CF=OD=AE=b,DF=OA=BE=a,
设A(a,0),D(0,b),
则B(a+b,a),C(b,a+b),
可得:b(a+b)=4,a(a+b)=4,
解得:a=b=$\sqrt{2}$.
所以点C的坐标为:($\sqrt{2}$,2$\sqrt{2}$).
点评 此题属于反比例函数的综合题,考查了待定系数法求函数的解析式、正方形的性质与判定、全等三角形的判定与性质以及勾股定理等知识.此题难度较大,综合性很强,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
14.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(-a,b)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.下列判断正确的是( )
| A. | 若一个数的绝对值是它的相反数,则这个数为负数 | |
| B. | 任何数的绝对值都是正数 | |
| C. | 两个数的绝对值相等,则这两个数相等 | |
| D. | 一个正数的绝对值一定是正数 |
16.等腰三角形的两边的长分别为2cm和7cm,则三角形的周长是( )
| A. | 11 | B. | 16 | C. | 11或16 | D. | 无法计算 |
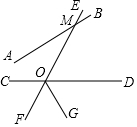 如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=$\frac{1}{2}$∠COF.
如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=$\frac{1}{2}$∠COF.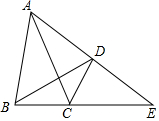 如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.
如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.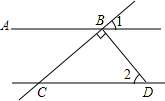 如图,直线AB∥CD,BC⊥BD于点B,∠1=40°,求∠2的度数.
如图,直线AB∥CD,BC⊥BD于点B,∠1=40°,求∠2的度数.