题目内容
16.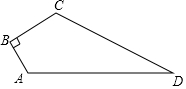 某单位有一块四边形的空地,∠B=90°,量得各边的长度AB=3米,BC=4米,CD=12米,AD=13米,现计划在空地内种草.
某单位有一块四边形的空地,∠B=90°,量得各边的长度AB=3米,BC=4米,CD=12米,AD=13米,现计划在空地内种草.(1)连接AC,证明△ACD是直角三角形;
(2)若每平方米草地造价30元,这块地全部种草的费用是多少元?
分析 (1)连接AC,在直角三角形ABC中可求得AC的长,由AC、AD、CD的长度关系由勾股定理的逆定理可得△ACD是直角三角形;
(2)四边形ABCD的面积=Rt△ABC的面积+Rt△ACD的面积,再把求出的面积乘以30即可求解.
解答  (1)证明:连接AC,
(1)证明:连接AC,
在Rt△ABC中,AC2=AB2+BC2=32+42=52,
AC=5,
在△ACD中,CD2=122,AD2=132,
而122+52=132,
即CD2+AC2=AD2,
∴∠ACD=90°,
∴△ACD是直角三角形;
(2)解:S四边形ABCD=S△ABC+S△ACD=$\frac{1}{2}$AB•BC+$\frac{1}{2}$CD•AC=$\frac{1}{2}$×3×4+$\frac{1}{2}$×12×5=36(平方米),
所以需费用36×30=1080(元).
故这块地全部种草的费用是1080元.
点评 本题考查了勾股定理的应用,通过勾股定理由边与边的关系也可证明直角三角形,这样解题较为简单.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
5.下列各组数是勾股数的是( )
| A. | 4,5,6 | B. | 6,8,10 | C. | 5,9,12 | D. | 6,9,13 |
7.下列方程①x-2=$\frac{1}{x}$;②x=0;③2x-y=3;④x2-3x=0;⑤x2-2x=3-3x+x2;⑥$\frac{x}{3}$=2x-1,其中是一元一次方程的是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
1.民兴中学某班教室有50人在开家长会,其中有3名老师,12名家长,35名学生.校长在门外听到有人在发言,
那么发言人是老师或学生的概率为( )
那么发言人是老师或学生的概率为( )
| A. | $\frac{19}{25}$ | B. | $\frac{3}{10}$ | C. | $\frac{47}{50}$ | D. | $\frac{1}{2}$ |
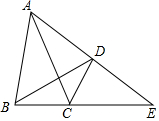 如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.
如图,已知在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.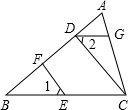 如图,CD⊥AB,EF⊥AB,垂足分别为D,F,∠1=∠2=50°.
如图,CD⊥AB,EF⊥AB,垂足分别为D,F,∠1=∠2=50°.