题目内容
8.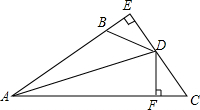 如图,已知DE⊥AB垂足为E,DF⊥AC垂足为F,BD=CD,BE=CF.
如图,已知DE⊥AB垂足为E,DF⊥AC垂足为F,BD=CD,BE=CF.(1)求证:AD平分∠BAC;
(2)丁丁同学观察图形后得出结论:AB+AC=2AE,请你帮他写出证明过程.
分析 (1)根据HL定理求出Rt△BED≌Rt△CFD,根据全等三角形的性质得出DE=DF,根据角平分线性质得出即可;
(2)证Rt△AED≌Rt△AFD,根据全等得出AE=AF,即可求出答案.
解答 证明:(1)∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中,
$\left\{\begin{array}{l}{BD=CD}\\{BE=CF}\end{array}\right.$,
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴∠EAD=∠CAD,
∴AD平分∠BAC;
(2)∵∠E=∠AFD=90°,
在Rt△AED和Rt△AFD中
$\left\{\begin{array}{l}{AD=AD}\\{DE=DF}\end{array}\right.$,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵BE=CF,
∴AB+AC=AE-BE+AF+CF=AE-CF+AE+CF=2AE.
点评 本题考查了全等三角形的性质和判定,角平分线性质的应用,能正确根据全等三角形的判定和性质定理进行推理是解此题的关键.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
3.下列四个图形中,轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
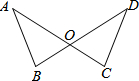 已知:如图AC=BD,AB=DC.证明:
已知:如图AC=BD,AB=DC.证明: