题目内容
18.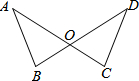 已知:如图AC=BD,AB=DC.证明:
已知:如图AC=BD,AB=DC.证明:(1)∠A与∠D;
(2)OB=OC.
分析 (1)连接BC,根据SSS推出△BCD≌△CBA,根据全等三角形的性质得出即可;
(2)根据全等三角形的性质得出∠ACB=∠DBC,根据等角对等边得出即可.
解答 证明:(1)连结BC,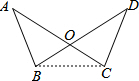
在△BCD和△CBA中,
$\left\{\begin{array}{l}{CD=AB}\\{BC=BC}\\{BD=AC}\end{array}\right.$,
∴△BCD≌△CBA(SSS),
∴∠A=∠D;
(2)∵△BCD≌△CBA,
∴∠ACB=∠DBC,
∴OB=OD.
点评 此题主要考查了全等三角形的判定和性质定理,等腰三角形的性质的应用,关键是找出能使三角形全等的条件,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
8.在二次根式$\sqrt{8}$,$\sqrt{5a}$,$\sqrt{\frac{c}{2}}$,$\sqrt{{m}^{2}+{n}^{2}}$,$\sqrt{{b}^{3}}$中,最简二次根式共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.一件衣服按原价的八折出售,价格为a元,则这件衣服的原价为( )
| A. | $\frac{a}{80%}$元 | B. | 80%a元 | C. | 20%a元 | D. | $\frac{a}{20%}$元 |
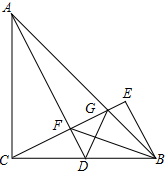 如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD,求证:
如图,△ABC中,AC=BC,∠ACB=90°,点D为BC的中点,点E与点C关于直线AD对称,CE与AD、AB分别交于点F、G,连接BE、BF、GD,求证: 如图,∠B=∠D,∠BAC=∠DAC,求证:△ABC≌△ADC.
如图,∠B=∠D,∠BAC=∠DAC,求证:△ABC≌△ADC.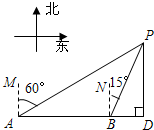 一艘轮船向正东航行,在A处测得灯塔P在A的北偏东60°方向,航行2小时到达B处,此时测得灯塔P在B的北偏东15°方向上,且灯塔P到轮船航线的距离PD是(10+10$\sqrt{3}$)海里,则轮船的航行速度为20海里/小时.
一艘轮船向正东航行,在A处测得灯塔P在A的北偏东60°方向,航行2小时到达B处,此时测得灯塔P在B的北偏东15°方向上,且灯塔P到轮船航线的距离PD是(10+10$\sqrt{3}$)海里,则轮船的航行速度为20海里/小时.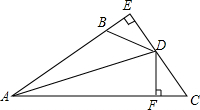 如图,已知DE⊥AB垂足为E,DF⊥AC垂足为F,BD=CD,BE=CF.
如图,已知DE⊥AB垂足为E,DF⊥AC垂足为F,BD=CD,BE=CF.