题目内容
6.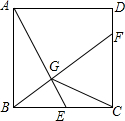 如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为$\sqrt{5}$-1.
如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为$\sqrt{5}$-1.
分析 取AB得中点O,连接OC,根据题意,G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,所以OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,根据勾股定理求出最小CG长度即可.
解答 解:取AB得中点O,连接OC,
根据题意,G点的轨迹是以AB中点O为圆心,AO为半径的圆弧,所以OC和OG的长度是一定的,因此当O、G、C在同一条直线上时,CG取最小值,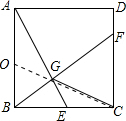
∵四边形ABCD是正方形,
∴∠ABC=90°,
∵正方形ABCD的边长为2,
∴BO=1,BC=2,
∴OC=$\sqrt{O{B}^{2}+B{C}^{2}}$=$\sqrt{5}$,
∴CG的最小值为OC-OG=$\sqrt{5}$-1,
故答案为:$\sqrt{5}$-1.
点评 本题考查了正方形的性质以及勾股定理的运用,根据题意,得到G点的轨迹是以AB中点O为圆心,AO为半径的圆弧是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.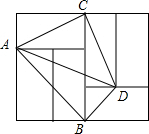 如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的特点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin∠BAD的值为( )
如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的特点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin∠BAD的值为( )
 如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的特点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin∠BAD的值为( )
如图,由6个形状、大小完全相同的小矩形组成矩形网络,小矩形的顶点称为这个矩形网络的特点,已知小矩形较短边长为1,点A,B,C,D都在格点上,则sin∠BAD的值为( )| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
15.给出下列函数:①y=2x;②y=-2x+1;③y=$\frac{2}{x}$(x>0);④y=x2(x<1),其中y随x的增大而减小的函数是( )
| A. | ①②③④ | B. | ②③④ | C. | ②④ | D. | ②③ |
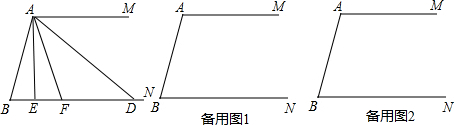
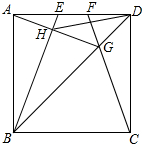 如图,E、F是正方形ABCD的边AD上有两个动点,满足AE=DF,连接CF交BD于G,连接BE交AG于点H,若正方形的边长为3,则线段DH长度的最小值是$\frac{3}{2}$($\sqrt{5}$-1).
如图,E、F是正方形ABCD的边AD上有两个动点,满足AE=DF,连接CF交BD于G,连接BE交AG于点H,若正方形的边长为3,则线段DH长度的最小值是$\frac{3}{2}$($\sqrt{5}$-1).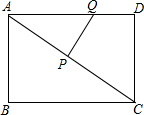 如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,矩形ABCD中,AB=6cm,BC=8cm,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(0<t<2),连接PQ.