题目内容
等腰三角形的一边长10,面积为40,则底角的正切值为 .
考点:解直角三角形,等腰三角形的性质
专题:分类讨论
分析:由题意知腰和底边不确定,应分两种情况进行讨论:(1)腰长为10;(2)底为10,进行求解.
解答: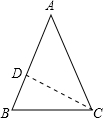 解:在△ABC中,AB=AC,∠B=∠C=∠α.
解:在△ABC中,AB=AC,∠B=∠C=∠α.
(1)当AB=10时,过A作CD⊥AB于D.
∵S△ABC=
AB•CD=40,
∴
×10•CD=40,
∴CD=8.
在Rt△ACD中,由勾股定理,得AD=
=6,
 BD=10-6=4,
BD=10-6=4,
∴底角tanα=
=2;
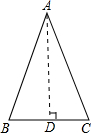
(2)当BC=10时,过A作AD⊥BC于D,则BD=5.
∵S△ABC=
BC•AD=40,
∴
×10•AD=40,
∴AD=8,
∴底角tanα=
=
.
综上可知底角的正切值为2或
.
故答案为2或
.
 解:在△ABC中,AB=AC,∠B=∠C=∠α.
解:在△ABC中,AB=AC,∠B=∠C=∠α.(1)当AB=10时,过A作CD⊥AB于D.
∵S△ABC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴CD=8.
在Rt△ACD中,由勾股定理,得AD=
| 102-82 |
 BD=10-6=4,
BD=10-6=4,∴底角tanα=
| CD |
| BD |
(2)当BC=10时,过A作AD⊥BC于D,则BD=5.
∵S△ABC=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴AD=8,
∴底角tanα=
| AD |
| BD |
| 8 |
| 5 |
综上可知底角的正切值为2或
| 8 |
| 5 |
故答案为2或
| 8 |
| 5 |
点评:本题考查了等腰三角形的性质,正切函数的定义.由于不确定腰长和底边,应分情况进行讨论.此题利用了分类讨论的思想.

练习册系列答案
相关题目
 如图,等腰△ABC,其中AB=BC,AB比AC长12cm,若△ABC的周长为96cm,求AC的长.
如图,等腰△ABC,其中AB=BC,AB比AC长12cm,若△ABC的周长为96cm,求AC的长. 已知梯形ABCD,AB∥CD,∠D=2∠B,AD=10,AB=15,求CD的长.
已知梯形ABCD,AB∥CD,∠D=2∠B,AD=10,AB=15,求CD的长. 如图,⊙O的直径为10,OC⊥AB于点D,CD=1,P为⊙O上一点,且PA⊥AB,连接PC,则tan∠APC=
如图,⊙O的直径为10,OC⊥AB于点D,CD=1,P为⊙O上一点,且PA⊥AB,连接PC,则tan∠APC=