题目内容
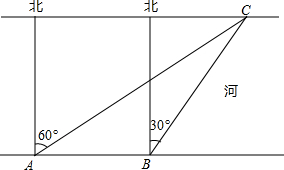
为了加快城市经济发展,某市准备修建一条横跨南北的大桥,如图所示,测量队在点A处观测河对岸水边有一点C,测得C在A处北偏东60°的方向上,沿河岸向东前行40米到达B处,测得C在B处北偏东30°的方向上,请你根据以上数据帮助该测量队计算出这条河的宽度(结果保留根号).

考点:解直角三角形的应用-方向角问题
专题:
分析:如图,过点C作CD⊥AB于D,由题意知道∠DAC=30°,∠DBC=60°,根据∠ACB=∠CBD-∠CAD=30°得到∠ACB=∠CAB,从而得到BC=AB=40米,然后在直角三角形CBD中利用解直角三角形求得CD的长即可.
解答: 解:如图,作CD⊥于AB于D.
解:如图,作CD⊥于AB于D.
由题意可知:AB=40米,∠CAD=30°,∠CBD=60°,
∴∠ACB=∠CBD-∠CAD=30°,
∴∠ACB=∠CAB,
∴BC=AB=40米.
在Rt△CBD中,CD=CB•sin60°=40×
=20
(米).
答:这条河的宽度为20
米.
 解:如图,作CD⊥于AB于D.
解:如图,作CD⊥于AB于D.由题意可知:AB=40米,∠CAD=30°,∠CBD=60°,
∴∠ACB=∠CBD-∠CAD=30°,
∴∠ACB=∠CAB,
∴BC=AB=40米.
在Rt△CBD中,CD=CB•sin60°=40×
| ||
| 2 |
| 3 |
答:这条河的宽度为20
| 3 |
点评:此题主要考查了解直角三角形-方向角问题,解题时首先正确理解题意,然后作出辅助线构造直角三角形解决问题.

练习册系列答案
相关题目
 一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的若干分内既进水又出水,之后只出水不进水.每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图.则a=
一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的若干分内既进水又出水,之后只出水不进水.每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图.则a= 如图,已知二次函数图象的顶点为(1,-3),并经过点C(2,0).
如图,已知二次函数图象的顶点为(1,-3),并经过点C(2,0).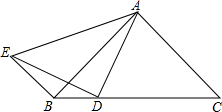 △ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE,AE和BE,AD=DE,BE∥AC.求证:∠BED=∠DAB.
△ABC中,AB=AC,D是BC边上一点,连接AD,E为△ABC外一点,连接DE,AE和BE,AD=DE,BE∥AC.求证:∠BED=∠DAB.