题目内容
5.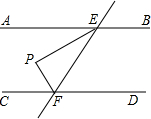 如图,AB∥CD,直线EF与AB,CD分别相交于点E、F,EP平分∠AEF,FP平分∠EFC.
如图,AB∥CD,直线EF与AB,CD分别相交于点E、F,EP平分∠AEF,FP平分∠EFC.(1)求证:△EPF是直角三角形;
(2)若∠PEF=30°,直接写出∠PFC的度数.
分析 (1)根据平行线的性质,由AB∥CD得到∠AEF+∠CFE=180°,再根据角平分线定义得∠PEF+∠PFE=$\frac{1}{2}$(∠AEF+∠CFE),然后计算出∠EPF=90°,根据垂直的定义即可得到△EPF是直角三角形;
(2)根据三角形内角和定理进行计算即可.
解答 解:(1)∵AB∥CD,
∴∠AEF+∠CFE=180°,
又∵EP平分∠AEF,FP平分∠EFC,
∴∠PEF+∠PFE=$\frac{1}{2}$(∠AEF+∠CFE)=$\frac{1}{2}$×180°=90°,
∴△EPF是直角三角形;
(2)∵△EPF是直角三角形,∠PEF=30°,
∴∠PFE=90°-30°=60°.
点评 本题考查了平行线性质,角平分线定义的运用,解题时注意:两直线平行,同旁内角互补.

练习册系列答案
相关题目
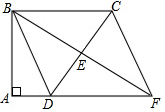 如图,四边形ABCD中,∠A=∠ABC=90°,AD=3,BC=5,E是边CD的中点,连结BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=3,BC=5,E是边CD的中点,连结BE并延长与AD的延长线相交于点F.