题目内容
12. 在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).
在平面直角坐标系中,A,B,C三点的坐标分别为(-5,4),(-3,0),(0,2).(1)画出三角形ABC,并求三角形ABC的面积;
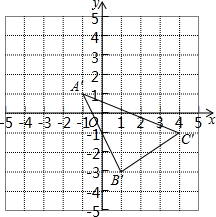
(2)如图,三角形A′B′C′可以由三角形ABC经过怎样的平移得到?对应点的坐标有什么变化?
(3)已知点P(m,n)为三角形ABC内的一点,则点P在三角形A′B′C′内的对应点P′的坐标为(m+4,n-3)
分析 (1)找出点A、B、C的位置,连接AB、BC、AC可得到三角形ABC,然后依据△ABC的面积等于矩形的面积减去3个直角三角形的面积求解即可.
(2)先确定出点A′的坐标,然后依据点A与点A′的位置可确定出平移的方向和距离;
(3)依据平移与坐标变化的规律求解即可.
解答 解:(1)如图1所示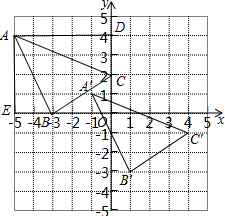
S△ABC=S矩形AEOD-S△ADC-S△BCO-S△AEB
=4×5-$\frac{1}{2}$×5×2-$\frac{1}{2}$×3×2-$\frac{1}{2}$×4×2
=20-5-3-4
=8.
(2)∵A(-5,4),A′(-1,1),
∴点A′由点A向右平移4个单位,然后向下平移3个单位得到.
∴△A′B′C′由△ABC向右平移4个单位,然后向下平移3个单位得到.
(3)点P(m,n)对应点P′的坐标为(m+4,n-3).
故答案为:(m+4,n-3).
点评 本题主要考查的是平移与坐标变化,掌握平移与坐标变化的规律是解题的关键.

练习册系列答案
相关题目
7.若点P(a-2,a)在第二象限,则a的取值范围是( )
| A. | 0<a<2 | B. | -2<a<0 | C. | a>2 | D. | a<0 |
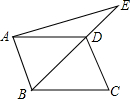 如图,点E在平行四边形ABCD的对角线BD的延长线上.
如图,点E在平行四边形ABCD的对角线BD的延长线上. 如图,直线l与直线a,b相交,且a∥b,∠1=45°,则∠2的度数是45°.
如图,直线l与直线a,b相交,且a∥b,∠1=45°,则∠2的度数是45°.