题目内容
3.在△ABC中,∠C=90°,AC=5,BC=12,D为AC边的中点,E为BC边的中点.则DE=6.5.分析 先利用勾股定理计算出AB,然后根据三角形中位线定理求解.
解答 解:∵∠C=90°,AC=5,BC=12,
∴AB=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
∵D为AC边的中点,E为BC边的中点.
∴DE=$\frac{1}{2}$AB=6.5.
故答案为6.5.
点评 本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.

练习册系列答案
相关题目
15.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如表所示的优惠.例如:购买A类会员年卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数多于60次时,则最省钱的方式为( )
| 会员年卡类型 | 办卡费用(元) | 每次游泳收费(元) |
| A 类 | 50 | 25 |
| B 类 | 200 | 20 |
| C 类 | 400 | 15 |
| A. | 购买A类会员年卡 | B. | 购买B类会员年卡 | C. | 购买C类会员年卡 | D. | 不购买会员年卡 |
12.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
则当y>2时,x的取值范围是x<1或x>3.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
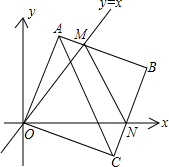 在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点,现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
 如图,D是△ABC边BC延长线上一点,DF⊥AB,垂足为F,且交AC于E,∠A=40°,∠D=25°,则∠1=75°.
如图,D是△ABC边BC延长线上一点,DF⊥AB,垂足为F,且交AC于E,∠A=40°,∠D=25°,则∠1=75°.