题目内容
2. 如图,反比例函数y=$\frac{{k}_{1}}{x}$的图象与一次函数y=k2x+b的图象交于点P(m,-1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ.
如图,反比例函数y=$\frac{{k}_{1}}{x}$的图象与一次函数y=k2x+b的图象交于点P(m,-1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ.(1)求两函数的解析式;
(2)求证:△POB≌△QOA.
分析 (1)将已知的点Q的坐标代入反比例函数,求得比例系数k1的值,得到反比例函数解析式;再将点P的坐标代入反比例函数,求得m的值,最后将点P和点Q的坐标代入一次函数,求得k2和b的值,得到一次函数解析式;
(2)先根据一次函数求得直线与与坐标轴的交点A、B的坐标,进而根据OA和OB的长相等,得到∠QAO=∠PBO;再根据点P、Q的坐标,求得OP与OQ的长,根据OP与OQ的长相等,得到∠BPO=∠AQO,最后根据AAS得到△POB≌△QOA.
解答  解:(1)将Q(1,2)代入反比例函数$y=\frac{{k}_{1}}{x}$,得k1=2
解:(1)将Q(1,2)代入反比例函数$y=\frac{{k}_{1}}{x}$,得k1=2
∴反比例函数的解析式为$y=\frac{2}{x}$
将P(m,-1)代入反比例函数$y=\frac{2}{x}$,得m=-2
∴P(-2,-1)
将P(-2,-1)和Q(1,2)代入一次函数y=k2x+b,得
$\left\{\begin{array}{l}{{k}_{2}+b=2}\\{-2{k}_{2}+b=-1}\end{array}\right.$
解得$\left\{\begin{array}{l}{{k}_{2}=1}\\{b=1}\end{array}\right.$
∴该一次函数的解析式为y=x+1
(2)∵y=x+1,当x=0时,y=1;当y=0时,x=-1
∴A(-1,0),B(0,1)
∴OA=OB
∴∠QAO=∠PBO
∵OP=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,OQ=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$
∴OP=OQ
∴∠BPO=∠AQO
∴△POB≌△QOA(AAS)
点评 本题主要考查了反比例函数与一次函数的交点以及全等三角形的判定,解决问题的关键是掌握待定系数法求函数解析式.当有两个函数的时候,着重使用两函数的交点坐标以及直线与坐标轴的交点坐标,体现了数形结合思想,综合性较强.本题也可以运用SSS判定两个三角形全等.

 如图,正五边形ABCDE中,以BC为一边,在五边形内部作等边△BCF,连结AF,则∠AFB的度数是( )
如图,正五边形ABCDE中,以BC为一边,在五边形内部作等边△BCF,连结AF,则∠AFB的度数是( )| A. | 72° | B. | 66° | C. | 65° | D. | 60° |




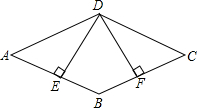 如图,已知四边形ABCD是菱形,DE⊥AB于E,DF⊥BC于F.求证:△ADE≌△CDF.
如图,已知四边形ABCD是菱形,DE⊥AB于E,DF⊥BC于F.求证:△ADE≌△CDF.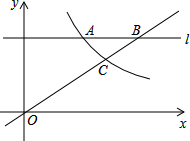 在平面直角坐标系中,反比例函数$y=\frac{k}{x}$的图象过点A($\frac{3}{2}$,2).
在平面直角坐标系中,反比例函数$y=\frac{k}{x}$的图象过点A($\frac{3}{2}$,2). 已知:如图,在△ABC中,CB=3,AB=4,AC=5,以点B为圆心的圆与AC相切于点D,则⊙B的半径为2.4.
已知:如图,在△ABC中,CB=3,AB=4,AC=5,以点B为圆心的圆与AC相切于点D,则⊙B的半径为2.4.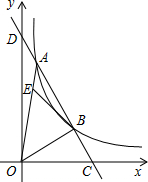 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$,点E在线段OA上一点,OE=3EA,若△AEB的面积为1,则k的值是3.
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$,点E在线段OA上一点,OE=3EA,若△AEB的面积为1,则k的值是3. 如图,小明利用暑假对他家所在阳光社区的居民进行了“小区绿化”满意情况的问卷调查,他在该社区随机抽取了200户居民,根据调查结果,将“小区绿化情况”绘制成如图条形统计图,若整个阳光社区共有居民3600户,根据上述统计数据,请你估计整个阳光社区对“小区绿化”不满意的居民有1440户.
如图,小明利用暑假对他家所在阳光社区的居民进行了“小区绿化”满意情况的问卷调查,他在该社区随机抽取了200户居民,根据调查结果,将“小区绿化情况”绘制成如图条形统计图,若整个阳光社区共有居民3600户,根据上述统计数据,请你估计整个阳光社区对“小区绿化”不满意的居民有1440户.