题目内容
7.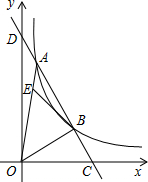 如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$,点E在线段OA上一点,OE=3EA,若△AEB的面积为1,则k的值是3.
如图,一次函数与反比例函数y=$\frac{k}{x}$(x>0)的图象在第一象限交于A、B两点,交x轴于点C,交y轴于点D,且$\frac{CB}{BA}$=$\frac{1}{2}$,点E在线段OA上一点,OE=3EA,若△AEB的面积为1,则k的值是3.
分析 过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,根据OE=3EA,S△AEB=1可得出S△AOB=4,设出点A、B的坐标,利用梯形的面积公式找出S梯形AMNB的值,通过分割图形找出S梯形AMNB=S△AOB,从而得出$\frac{{n}^{2}-{m}^{2}}{mn}k$=8①,再结合AM⊥x轴,BN⊥x轴得出AM∥BN,从而得出$\frac{BC}{AC}=\frac{BC}{BC+AB}$=$\frac{BN}{AM}$,由$\frac{CB}{BA}$=$\frac{1}{2}$即可得出n=3m②,联立①②成方程组,解方程即可得出结论.
解答 解:过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,如图所示.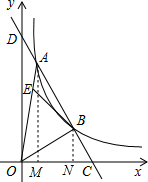
∵OE=3EA,S△AEB=1,
∴S△AOB=(3+1)S△AEB=4.
设点A的坐标为(m,$\frac{k}{m}$)、点B的坐标为(n,$\frac{k}{n}$),
则AM=$\frac{k}{m}$,BN=$\frac{k}{n}$,MN=n-m.
S梯形AMNB=$\frac{1}{2}$(AM+BN)•MN=$\frac{1}{2}$($\frac{k}{m}$+$\frac{k}{n}$)(n-m)=S△AOB=4,
即$\frac{{n}^{2}-{m}^{2}}{mn}k$=8①;
∵AM⊥x轴,BN⊥x轴,
∴AM∥BN,
∴$\frac{BC}{AC}=\frac{BC}{BC+AB}$=$\frac{BN}{AM}$.
∵$\frac{CB}{BA}$=$\frac{1}{2}$,
∴$\frac{BN}{AM}$=$\frac{\frac{k}{n}}{\frac{k}{m}}$=$\frac{1}{3}$,
∴n=3m②.
联立①②得:$\left\{\begin{array}{l}{n=3m}\\{\frac{{n}^{2}-{m}^{2}}{mn}k=8}\end{array}\right.$,解得:k=3.
故答案为:3.
点评 本题考查了反比例函数与一次函数的交点问题、三角形的面积公式、梯形的面积公式以及解三元二次方程组,解题的关键是找出关于m、n、k的方程组.本题属于中档题,难度不大,但稍显繁琐,本题巧妙的利用分割图形求面积法找出梯形的面积,再结合比例关系以及梯形的面积公式得出方程组是关键.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案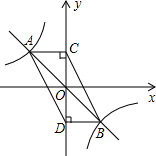 如图,正比例函数y=-x与反比例函数y=-$\frac{2}{x}$的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为C、D,连接AD,BC,则四边形ACBD的面积为( )
如图,正比例函数y=-x与反比例函数y=-$\frac{2}{x}$的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为C、D,连接AD,BC,则四边形ACBD的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
①若a>b,则c-a<c-b;
②若|a|=-a,则a<0;
③对角线互相平分且相等的四边形是菱形;
④直角三角形斜边上的中线等于斜边的一半.
其中原命题与逆命题均为真命题的是( )
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ③④ |
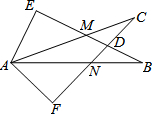 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.
其中正确结论的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 随着科技的发展,电动汽车的性能得到显著提高.某市对市场上电动汽车的性能进行随机抽样调查,抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据,绘制成如下两幅表和图.
随着科技的发展,电动汽车的性能得到显著提高.某市对市场上电动汽车的性能进行随机抽样调查,抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据,绘制成如下两幅表和图.| 组别 | 行驶的里程x(千米) | 频数(台) | 频率 |
| A | x<200 | 18 | 0.15 |
| B | 200≤x<210 | 36 | a |
| C | 210≤x<220 | 30 | |
| D | 220≤x<230 | b | |
| E | x≥230 | 12 | 0.10 |
| 合计 | c | 1.00 | |
(1)a=0.3,b=24,c=120;
(2)请将条形统计图补充完整;
(3)若该市市场上的电动汽车有2000台,请你估计电动汽车一次充电后行驶的里程数在220千米及以上的台数.
 如图,在平行四边形ABCD中,点E,F分别为边BC,AD的中点.求证:四边形AECF是平行四边形.
如图,在平行四边形ABCD中,点E,F分别为边BC,AD的中点.求证:四边形AECF是平行四边形. 如图,反比例函数y=$\frac{{k}_{1}}{x}$的图象与一次函数y=k2x+b的图象交于点P(m,-1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ.
如图,反比例函数y=$\frac{{k}_{1}}{x}$的图象与一次函数y=k2x+b的图象交于点P(m,-1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ.