题目内容
11. 如图,正五边形ABCDE中,以BC为一边,在五边形内部作等边△BCF,连结AF,则∠AFB的度数是( )
如图,正五边形ABCDE中,以BC为一边,在五边形内部作等边△BCF,连结AF,则∠AFB的度数是( )| A. | 72° | B. | 66° | C. | 65° | D. | 60° |
分析 根据多边形的内角和公式列式求出∠ABC,再根据等边三角形的每一个内角都是60°可得∠CBF=60°,三条边都相等可得BC=BF,然后求出∠ABF,AB=BF,最后根据等腰三角形两底角相等求解即可.
解答 解:在正五边形ABCDE中,∠ABC=$\frac{1}{5}$×(5-2)×180°=108°,
∵△BCF是等边三角形,
∴∠CBF=60°,BC=BF,
∴∠ABF=108°-60°=48°,
∵AB=BC,
∴AB=BF,
∴∠AFB=$\frac{1}{2}$(180°-∠ABF)=$\frac{1}{2}$(180°-48°)=66°.
故选B.
点评 本题考查了多边形的内角与外角,等边三角形的性质,等腰三角形的性质,熟记各性质并确定出最后的等腰三角形是解题的关键.

练习册系列答案
相关题目
1.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.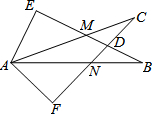 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:
①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.
其中正确结论的个数为( )
 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.
其中正确结论的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.门头沟地处北京西南部,山青水秀,风景如画,静谧清幽.近年来,某村依托丰富的自然资源和人文资源,大力开发建设以农业观光园为主的多类型休闲旅游项目,农民收入逐步提高.以下是根据该村公布的“主要经济发展指标”相关数据绘制的统计图表的一部分.
2012-2015年农业观光园经营年收入增长率统计表

根据以上信息解答下列问题:
(1)该村2013年农业观光园经营年收入的年增长率约是17%;(结果精确到1%)
(2)补全条形统计图,并在图中标明相应的数据;(结果精确到0.1)
(3)请预估该村2016年的农业观光园经营年收入约为33.9万元,你预估的理由是由条形统计图和表格可知,每年的增长率都在上升,2014年增长22%,2015年增长24%,故预估2016年的增长率为26%.
2012-2015年农业观光园经营年收入增长率统计表
| 年份 | 年增长率(精确到1%) |
| 2012年 | 12% |
| 2013年 | |
| 2014年 | 22% |
| 2015年 | 24% |

根据以上信息解答下列问题:
(1)该村2013年农业观光园经营年收入的年增长率约是17%;(结果精确到1%)
(2)补全条形统计图,并在图中标明相应的数据;(结果精确到0.1)
(3)请预估该村2016年的农业观光园经营年收入约为33.9万元,你预估的理由是由条形统计图和表格可知,每年的增长率都在上升,2014年增长22%,2015年增长24%,故预估2016年的增长率为26%.
 如图,反比例函数y=$\frac{{k}_{1}}{x}$的图象与一次函数y=k2x+b的图象交于点P(m,-1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ.
如图,反比例函数y=$\frac{{k}_{1}}{x}$的图象与一次函数y=k2x+b的图象交于点P(m,-1)和Q(1,2)两点,记一次函数与坐标轴的交点分别为A,B,连接OP,OQ. 如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,且AH=1,HB=2,BC=5,则$\frac{DE}{EF}$=$\frac{3}{5}$.
如图,直线l1∥l2∥l3,直线AC分别交l1、l2、l3于点A、B、C,直线DF分别交l1、l2、l3于点D、E、F,AC与DF相交于点H,且AH=1,HB=2,BC=5,则$\frac{DE}{EF}$=$\frac{3}{5}$.