题目内容
11.【结论】已知两条直线l1:y=k1x+b1,l2:y=k2x+b2,若l1⊥l2,则有k1•k2=-1,反之也成立.【应用】(1)已知y=3x+1与y=kx-1垂直,求k的值;
(2)已知直线m经过点A(2,3),且与y=$-\frac{1}{2}$x+3垂直,求直线m的解析式.
【探究】(3)在同一直角坐标系上,给定4个点A(1,3)、B(-3,0)、C(0,-4)和D(4,-1),任意连接其中两点能得到多少条不同的直线?这些直线中共有多少组互相垂直关系?并选择其中一组互相垂直关系进行证明.
分析 (1)根据若l1⊥l2,则有k1•k2=-1,即可求出k的值.
(2)先求出直线m的一次项系数,然后将(2,3)代入一次函数解析式即可求出m的值.
(3)根据四个点的坐标作出简图后进行判断,然后根据l1⊥l2,则有k1•k2=-1,即可进行证明.
解答 解:(1)∵l1⊥l2,则k1•k2=-1,
∴3k=-1,∴k=$-\frac{1}{3}$;
(2)∵过点A直线与y=$-\frac{1}{2}$x+3垂直,
∴设过点A直线的直线解析式为y=2x+b,
把A(2,3)代入得,b=-1,
∴解析式为y=2x-1.
(3)连接其中任意两点能得到6条直线,
这些直线中共有5组互相垂直关系,(它们分别是:AB⊥BC,BC⊥CD,CD⊥DA,DA⊥AB和AC⊥BD).
设直线BC为:y=k1x-4,将B(-3,0)代入得:0=-3k1-4
解得:${k_1}=-\frac{4}{3}$;
设直线CD为:y=k2x-4,将D(4,-1)代入得:-1=4k2-4
解得:${k_2}=\frac{3}{4}$;
∵${k_1}•{k_2}=-\frac{4}{3}×\frac{3}{4}=-1$,
∴BC⊥CD.
点评 本题考查一次函数的解析式,解题的关键是正确理解:若l1⊥l2,则有k1•k2=-1,本题考查学生的阅读理解能力,属于中等题型.

练习册系列答案
相关题目
16.若m是任意实数,则点A(m2+1,-4)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
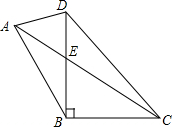 如图,在四边形ABCD中,∠DBC=90°,∠ABD=30°,∠ADB=75°,AC与BD交于点E,若CE=2AE=4$\sqrt{3}$,则DC的长为6$\sqrt{2}$.
如图,在四边形ABCD中,∠DBC=90°,∠ABD=30°,∠ADB=75°,AC与BD交于点E,若CE=2AE=4$\sqrt{3}$,则DC的长为6$\sqrt{2}$. 如图所示,经过圆内一点P作弦AB和CD,且DP=BP,求证:PA=PC.
如图所示,经过圆内一点P作弦AB和CD,且DP=BP,求证:PA=PC. 如图,在5×4的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个3个.
如图,在5×4的方格纸中,每个小正方形边长为1,点O、A、B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有个3个. 如图,在7×7网格中,每个小正方形的边长都为1.
如图,在7×7网格中,每个小正方形的边长都为1.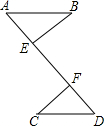 如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定 Rt△ABE≌Rt△DCF的是①②③(填入序号)
如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定 Rt△ABE≌Rt△DCF的是①②③(填入序号)