题目内容
3. 如图,在7×7网格中,每个小正方形的边长都为1.
如图,在7×7网格中,每个小正方形的边长都为1.(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为(-2,-1);
(2)△ABC的面积为5;
(3)判断△ABC的形状,并说明理由.
分析 (1)首先根据A和C的坐标确定坐标轴的位置,然后确定B的坐标;
(2)利用矩形的面积减去三个直角三角形的面积求解;
(3)利用勾股定理的逆定理即可作出判断.
解答 解:(1)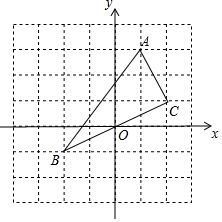
则B的坐标是(-2,-1).
故答案是(-2,-1);
(2)S△ABC=4×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×3×4-$\frac{1}{2}$×1×2=5,
故答案是:5;
(3)∵AC2=22+12=5,BC2=22+42=20,AB2=42+32=25,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°.
点评 本题考查了平面直角坐标系确定点的位置以及勾股定理的逆定理,正确确定坐标轴的位置是关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
13.如图,两个形状、大小完全相同的大长方形内放入四个如图③的小长方形后分别得到如图①、图②,已知大长方形的长为a,则图②阴影部分周长与图①阴影部分周长的差是( )
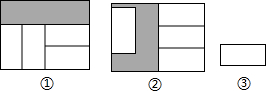

| A. | a | B. | $\frac{a}{3}$ | C. | $\frac{2}{3}$a | D. | $\frac{a}{2}$ |
14.一次函数y=mx+|m-1|的图象过点(0,2),且y随x的增大而减小,则m的值为( )
| A. | -1 | B. | 1 | C. | 3 | D. | -1或3 |