题目内容
15.甲、乙两地相距880千米小轿车从甲地出发,2小时后,大客车从乙地出发相向而行,又经过4小时两车相遇.已知小轿车比大客车每小时多行20千米.设大客车每小时行x千米,小轿车每小时行y千米,则可列方程组为( )| A. | $\left\{\begin{array}{l}{x-y=20}\\{6x+4y=880}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{y-x=20}\\{6y+4x=880}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y-x=880}\\{6y+4x=20}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{y-x=20}\\{4y+6x=880}\end{array}\right.$ |
分析 设大客车每小时行x千米,小轿车每小时行y千米,根据小轿车比大客车每小时多行20千米,甲车行驶2小时,两车相向行驶4小时共走了880千米,据此列方程组求解、
解答 解:设大客车每小时行x千米,小轿车每小时行y千米,
由题意得,$\left\{\begin{array}{l}{y-x=20}\\{4x+6y=880}\end{array}\right.$.
故选B.
点评 本题考查了由实际问题抽象出二元一次方程组,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程组求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.实数m,n满足(m+n)2+m+n-2=0,则(m+n)2的值为( )
| A. | 1或-2 | B. | 1 | C. | 1或2 | D. | 1或4 |
10. 不能判定四边形ABCD为平行四边形的题设是( )
不能判定四边形ABCD为平行四边形的题设是( )
 不能判定四边形ABCD为平行四边形的题设是( )
不能判定四边形ABCD为平行四边形的题设是( )| A. | AB=CD,AB∥CD | B. | ∠A=∠C,∠B=∠D | C. | AB=AD,BC=CD | D. | AB=CD,AD=BC |
 如图,∠AOC=90°,∠BOD=90°,且∠BOC=40°,则∠AOD=140°.
如图,∠AOC=90°,∠BOD=90°,且∠BOC=40°,则∠AOD=140°.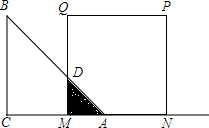 如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右平移,直到C点与M点重合时为止.设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm.
如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右平移,直到C点与M点重合时为止.设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm.