题目内容
17. 如图,已知直线AB、CD相交于点O,∠DOE=90°,
如图,已知直线AB、CD相交于点O,∠DOE=90°,①在∠1,∠2,∠3,∠4中,
对顶角有∠1和∠2,
邻补角有∠1和∠4,∠2和∠4,
②若∠1=50°,分别求出∠2、∠3、∠4的度数.
分析 ①根据对顶角和邻补角的定义得出即可;
②根据对顶角和邻补角的定义即可求出∠2和∠4,求出∠EOC,即可求出∠3.
解答 解:①在∠1,∠2,∠3,∠4中,
对顶角有∠1和∠2,
邻补角有∠1和∠4,∠2和∠4,
故答案为:∠1和∠2,∠1和∠4,∠2和∠4;
②∵∠1=50°,
∴∠2=∠1=50°,∠4=180°-∠1=130°,
∵∠DOE=90°,
∴∠EOC=90°,
∴∠3=90°-∠1=40°.
点评 本题考查了对顶角和邻补角的应用,能理解对顶角和邻补角的定义是解此题的关键,注意:对顶角相等,如果∠1和∠2是邻补角,那么∠1+∠2=180°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.为了考察甲、乙两种小麦的长势,分别从中随机抽取l0株麦苗,测得苗高(单位:cm)如表:
(1)分别计算两种小麦的平均苗高;
(2)哪种小麦的长势比较整齐?
| 甲 | 12 | 13 | 14 | 15 | 10 | 16 | 13 | 11 | 15 | 11 |
| 乙 | 11 | 16 | 17 | 14 | 13 | 19 | 6 | 8 | 10 | 16 |
(2)哪种小麦的长势比较整齐?
 如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,
如图,△ABC中,CD是∠ACB的角平分线,CE是AB边上的高, 如图是某种货车自动卸货时的示意图,AC是水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC的夹角为30°,举升杠杆OB与底盘AC的夹角为75°,已知O与A的距离为4米,试求货车卸货时举升杠杆OB的长($\sqrt{2}≈1.414$,精确到0.01米).
如图是某种货车自动卸货时的示意图,AC是水平汽车底盘,OB是液压举升杠杆,货车卸货时车厢AB与底盘AC的夹角为30°,举升杠杆OB与底盘AC的夹角为75°,已知O与A的距离为4米,试求货车卸货时举升杠杆OB的长($\sqrt{2}≈1.414$,精确到0.01米).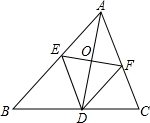 如图,△ABC的∠BAC的平分线AD被EF垂直平分,且E、F分别在AB,AC上,求证:四边形AEDF是菱形.
如图,△ABC的∠BAC的平分线AD被EF垂直平分,且E、F分别在AB,AC上,求证:四边形AEDF是菱形.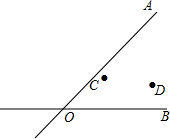 在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)
在加快城镇建设中,有两条公路OA和OB交汇于O点,在图中∠AOB的内部有蔬菜基地C和D,现要修建一个蔬菜转运站P,使转运站P到两条公路OA、OB的距离相等,且到两个蔬菜基地C、D的距离相等,用尺规作出蔬菜转运站P的位置.(要求:不写作法,保留作图痕迹.)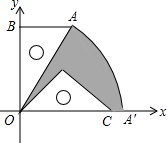 已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.
已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3. 2016年全国中小学生“安全教育日”主题:“强化安全意识,提升安全素养”,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
2016年全国中小学生“安全教育日”主题:“强化安全意识,提升安全素养”,小刚骑单车上学,当他骑了一段,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校.以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题: