题目内容
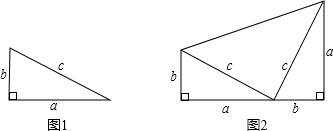
如图所示，以Rt△ABC的三条边为直径分别向外作半圆，设以BC为直径的半圆的面积记作S1，以AC为直径的半圆的面积记作S2，以AB为直径的半圆的面积记作S3，则S1、S2、S3之间的关系正确的是（ ）| A、S1+S2＞S3 |
| B、S1+S2＜S3 |
| C、S1+S2=S3 |
| D、无法确定 |
考点：勾股定理
专题：
分析：根据勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．以及圆的面积公式，即可求出S1、S2、S3之间的关系．
解答：解：∵S1=
π•（
）2=
=
π•BC2，
S2=
π•（
）2=
π•AC2，
S3=
π•（
）2=
π•AB2，
又∵BC2+AC2=AB2，
∴
π•BC2+
π•AC2=
π•AB2，
∴S1+S2=S3．
故选：C．
| 1 |
| 2 |
| BC |
| 2 |
| 1 |
| 8 |
| 1 |
| 8 |
S2=
| 1 |
| 2 |
| AC |
| 2 |
| 1 |
| 8 |
S3=
| 1 |
| 2 |
| AB |
| 2 |
| 1 |
| 8 |
又∵BC2+AC2=AB2，
∴
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
∴S1+S2=S3．
故选：C．
点评：本题考查了勾股定理和圆的面积公式，在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
练习册系列答案
相关题目
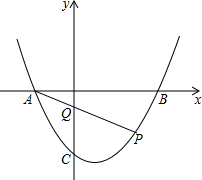如图，抛物线y=x2-2x-3与x轴交于A，B两点（A点在B点左侧），若点P为抛物线上一点，连AP交y轴于Q，且AP•AQ=4，求点P的坐标．
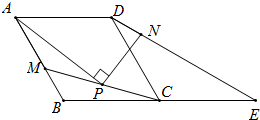已知如图，四边形ABCD是菱形，∠ABC=120°，△DCE是等腰三角形，CD=CE，点B、C、E在一条直线上，点M是AB上的一点，P是线段MC的中点，PA⊥PN，点N在DE上．
