题目内容
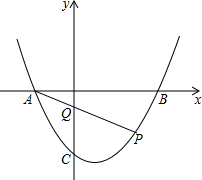 如图,抛物线y=x2-2x-3与x轴交于A,B两点(A点在B点左侧),若点P为抛物线上一点,连AP交y轴于Q,且AP•AQ=4,求点P的坐标.
如图,抛物线y=x2-2x-3与x轴交于A,B两点(A点在B点左侧),若点P为抛物线上一点,连AP交y轴于Q,且AP•AQ=4,求点P的坐标.考点:抛物线与x轴的交点
专题:
分析:设直线AP的解析式为y=k(x+1)(k≠0),求出点Q的坐标,与抛物线解析式联立求出点P的坐标,然后利用勾股定理列式表示出AQ、AP,再相乘解方程求出k值,然后解答即可.
解答:解:设直线AP的解析式为y=k(x+1)(k≠0),
则点Q的坐标为(0,k),
联立
,
解得
,
,
所以,点P的坐标为(k+3,k(k+4)),
由勾股定理得,AQ=
,AP=
=(k+4)
,
∵AP•AQ=4,
∴(k+4)
•
=4,
∴(k+4)(1+k2)=4,
整理得,k(k2+4k+1)=0,
解得k1=0(舍去),k2=-2-
(舍去),k3=-2+
,
∴k+3=-2+
+3=1+
,
k(k+4)=(-2+
)(-2+
+4)=-1,
∴点P的坐标为(1+
,-1).
则点Q的坐标为(0,k),
联立
|
解得
|
|
所以,点P的坐标为(k+3,k(k+4)),
由勾股定理得,AQ=
| 1+k2 |
| (k+3+1)2+[k(k+4)]2 |
| 1+k2 |
∵AP•AQ=4,
∴(k+4)
| 1+k2 |
| 1+k2 |
∴(k+4)(1+k2)=4,
整理得,k(k2+4k+1)=0,
解得k1=0(舍去),k2=-2-
| 3 |
| 3 |
∴k+3=-2+
| 3 |
| 3 |
k(k+4)=(-2+
| 3 |
| 3 |
∴点P的坐标为(1+
| 3 |
点评:本题考查了抛物线与x轴的交点,主要利用了联立两函数解析式求交点问题,勾股定理,设出直线解析式并列出关于k的方程是解题的关键.

练习册系列答案
相关题目
 如图所示,以Rt△ABC的三条边为直径分别向外作半圆,设以BC为直径的半圆的面积记作S1,以AC为直径的半圆的面积记作S2,以AB为直径的半圆的面积记作S3,则S1、S2、S3之间的关系正确的是( )
如图所示,以Rt△ABC的三条边为直径分别向外作半圆,设以BC为直径的半圆的面积记作S1,以AC为直径的半圆的面积记作S2,以AB为直径的半圆的面积记作S3,则S1、S2、S3之间的关系正确的是( )| A、S1+S2>S3 |
| B、S1+S2<S3 |
| C、S1+S2=S3 |
| D、无法确定 |
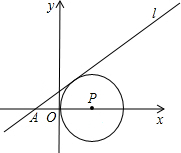 如图,点P在x轴上,OP=2,以点P为圆心,OP长为半径作圆,已知经过点A(-2,0)的直线l的函数解析式为y=kx+b,当l分别与⊙P相交、相切、相离时,求b的取值范围.
如图,点P在x轴上,OP=2,以点P为圆心,OP长为半径作圆,已知经过点A(-2,0)的直线l的函数解析式为y=kx+b,当l分别与⊙P相交、相切、相离时,求b的取值范围.