题目内容
15.如图①,直线l1、l2相交于点O,长为2的线段AB在直线l2上,点P是直线l1上一点,且∠APB=30°.(1)请在图①中作出符合条件的点P(不写画法,保留作图痕迹);
(2)若直线l1、l2的夹角为60°,线段AB在直线l2上左右移动.
①当OA的长为多少时,符合条件的点P有且只有一个?请说明理由;
②是否存在符合条件的点P有三个的情况?若存在,求出OA的长;若不存在,请说明理由.
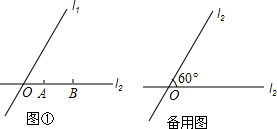
分析 (1)利用圆周角定理进而得出符合条件的点P;
(2)①利用当直线l1与⊙C相切于点P,且A在O的右侧时以及当直线l1与⊙C相切于点P,且A在O的左侧时分别得出符合题意的答案;
②利用当直线l1与⊙C1相交于点P1、P2,与⊙C2相切于点P3时,当直线l1与⊙C1相切于点P1,与⊙C2相交于点P2、P3时,分别得出即可.
解答 解:(1)如图①: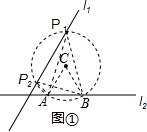
以AB为边在x轴上方作等边三角形ABC,以C为圆心,AB长为半径作圆,
与直线l1有两个交点P1、P2,则P1、P2是符合条件的点;
(2)①如备用图①,
当直线l1与⊙C相切于点P,且A在O的右侧时,则∠APB=30°
连接CP,过A作AD⊥l1于D
则AD=CP=2,∴OA=$\frac{AD}{sin60°}$=$\frac{4}{3}$$\sqrt{3}$,
如备用图②,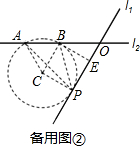
当直线l1与⊙C相切于点P,且A在O的左侧时,则∠APB=30°
连接CP,过B作BE⊥l1于E,
则BE=CP=2,∴OB=$\frac{BE}{sin60°}$=$\frac{4}{3}$$\sqrt{3}$,
∴OA=$\frac{4}{3}$$\sqrt{3}$+2,
综上所述,当A在O的右侧,OA=$\frac{4}{3}$$\sqrt{3}$或A在O的左侧,OA=$\frac{4}{3}$$\sqrt{3}$+2时符合条件的点P有且只有一个;
②存在,
如备用图③,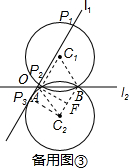
当直线l1与⊙C1相交于点P1、P2,与⊙C2相切于点P3时,连接C2P3,
过O作OF⊥BC2于F,则OF=C2P3=2,
∴OB=$\frac{BE}{sin60°}$=$\frac{4}{3}$$\sqrt{3}$,
∴OA=$\frac{4}{3}$$\sqrt{3}$-2,
如备用图④,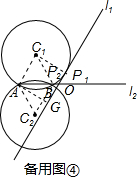
当直线l1与⊙C1相切于点P1,与⊙C2相交于点P2、P3时,连接C1P1,过A作AG⊥l1于G
则AG=C1P1=2,∴OA=$\frac{AG}{sin60°}$=$\frac{4}{3}$$\sqrt{3}$,
综上所述,当A在O的右侧,OA=$\frac{4}{3}$$\sqrt{3}$-2或A在O的左侧,OA=$\frac{4}{3}$$\sqrt{3}$时,符合条件的点P有三个.
点评 此题主要考查了圆的综合以及圆周角定理和切线的性质以及锐角三角函数关系等知识,利用分类讨论以及数形结合得出是解题关键.

 名校课堂系列答案
名校课堂系列答案| A. | 0 | B. | -2 | C. | 0或-2 | D. | -1或1 |
 在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为5•($\frac{3}{2}$)4022.
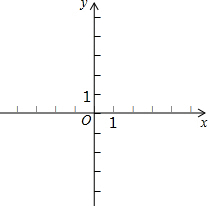 (1)在所给平面直角坐标系中,画出反比例函数y=$\frac{4}{x}$的图象;
(1)在所给平面直角坐标系中,画出反比例函数y=$\frac{4}{x}$的图象;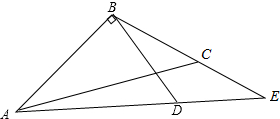 已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.
已知,如图,△ABC中,BD⊥AB于点B,AD的延长线交BC于点E.若∠CAE=∠CBD,∠EAB-∠BCA=10°,求出∠BAD的度数.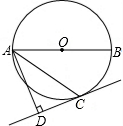 如图,AB是⊙O的直径,C为⊙O上一点,AD和过点C的切线CD垂直,垂足为点D.求证:AC平分∠BAD.
如图,AB是⊙O的直径,C为⊙O上一点,AD和过点C的切线CD垂直,垂足为点D.求证:AC平分∠BAD.