题目内容
10.动手实验:利用矩形纸片(如图1)剪出一个正六边形纸片;再利用这个正六边形纸片做一个无盖的正六棱柱(棱柱底面为正六边形),如图2.(1)做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为多少?
(2)在(1)的条件下,当矩形的长为2a时,要使无盖正六棱柱侧面积最大,正六棱柱的高为多少?并求此时矩形纸片的利用率为多少?(矩形纸片的利用率=$\frac{无盖正六棱柱的表面积}{矩形纸片的面积}$)
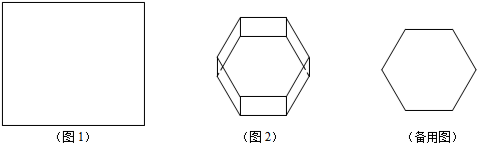
分析 (1)画出图形,利用正六边形的性质,设出矩形的长宽和正六边形的半径,利用特殊角的三角函数用正六边形的半径表示出矩形的长与宽解决问题;
(2)利用(1)中的边关系,设出正六边形高为x,表示出正六边形的面积,利用二次函数的性质解决问题.
解答 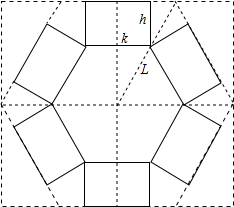 解:(1)如图所示:
解:(1)如图所示:
由于正六边形内角和为(6-2)×180°=720°,则其一角的角平分线所分的两个角同为60°;
设所需矩形的长宽分别为A、B,剪出的正六边形半径长为L,那么
A=2L,B=2L•sin60°=$\sqrt{3}$L;
因此,所求长宽比为A:B=(2L):($\sqrt{3}$L)=2:$\sqrt{3}$.
做一个这样的正六棱柱所需最小的矩形纸片的长与宽的比为:2:$\sqrt{3}$;
(2)∵矩形的长为2a,宽为:$\sqrt{3}$a,
∴正六边形边长为a,其面积为:S,
设高为x,S=-4$\sqrt{3}$x2+6ax,
当x=$\frac{\sqrt{3}}{4}$a时,S=$\frac{3\sqrt{3}}{4}$a2,
此时,底面积=$\frac{3\sqrt{3}}{8}$a2,S=$\frac{3\sqrt{3}}{4}$a2+$\frac{3\sqrt{3}}{8}$a2=$\frac{9\sqrt{3}}{8}$a2,
故利用率=$\frac{\frac{9\sqrt{3}}{8}{a}^{2}}{2\sqrt{3}{a}^{2}}$=$\frac{9}{16}$.
点评 此题考查正多边形的性质运用以及二次函数的实际运用,注意利用面积建立模型,解决实际问题.

练习册系列答案
相关题目
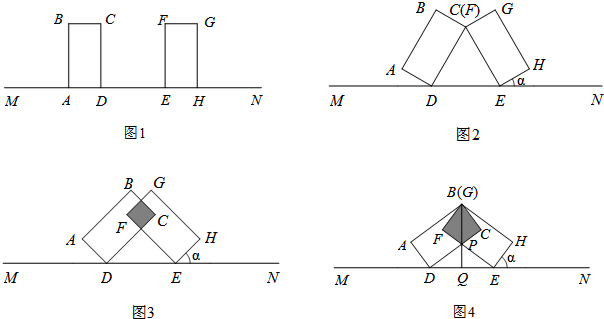
19. 把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )
把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )
 把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )
把一副直角三角板ABC(含30°、60°角)和CDE(含45°、45°角)如图放置,使直角顶点C重合,若DE∥BC,则∠1的度数是( )| A. | 75° | B. | 105° | C. | 110° | D. | 120° |
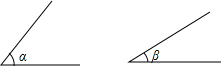 如图所示,已知∠α,∠β,且∠α,∠β均为锐角,求∠AOB,使它等于∠α与∠β的和.
如图所示,已知∠α,∠β,且∠α,∠β均为锐角,求∠AOB,使它等于∠α与∠β的和.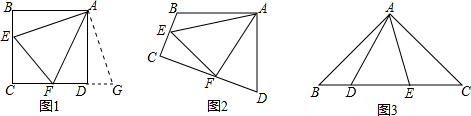
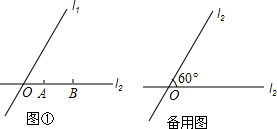
 如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求:
如图,若要建一个长方形鸡场,鸡场的一边靠墙,墙对面有一个2米宽的门,另三边用竹篱笆围成,篱笆总长33米,围成长方形的鸡场除门之外四周不能有空隙.求: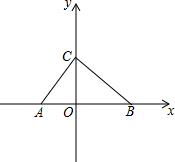 如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).
如图所示,点A、B、C的坐标分别为(-$\sqrt{2}$,0),(2$\sqrt{2}$,0),(0,2).