题目内容
 如图,P为⊙O的直径AB反向延长线上一点,PQ切⊙O于点Q,若tan∠P=
如图,P为⊙O的直径AB反向延长线上一点,PQ切⊙O于点Q,若tan∠P=| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:切线的性质,勾股定理,相似三角形的判定与性质,锐角三角函数的定义
专题:计算题
分析:连接OQ,AQ,过A作AM⊥PQ,由PQ为圆O的切线,利用切线的性质得到PQ垂直于OQ,在直角三角形OPQ中,利用锐角三角函数定义表示出tanP,设OQ=3k,得到PQ=4k,利用勾股定理得到OP=5k,由OP-OA表示出AP,再由一对直角相等,一对公共角,得到三角形APM与三角形OPQ相似,由相似得比例,表示出AM,在直角三角形APM中,利用勾股定理表示出PM,由PQ-PM表示出MQ,由弦切角等于夹弧所对的圆周角得到∠PQA=∠B,可得出tan∠PQA=tanB,在直角三角形AQM中,利用锐角三角函数定义求出tan∠PQA的值,即为tanB的值.
解答: 解:连接OQ,AQ,过A作AM⊥PQ,如图所示:
解:连接OQ,AQ,过A作AM⊥PQ,如图所示:
∵PQ为圆O的切线,
∴OQ⊥PQ,
在Rt△OPQ中,tanP=
=
,
设OQ=3k,则PQ=4k,根据勾股定理得:OP=5k,
AP=OP-OA=5k-3k=2k,
∵∠OQP=∠AMP=90°,∠P=∠P,
∴△APM∽△OPQ,
∴
=
,
∴AM=
=
k,
在Rt△APM中,AP=2k,AM=
k,
根据勾股定理得:PM=
=
k,
∴MQ=PQ-PM=4k-
k=
k,
∵∠PQA=∠B,
∴tanB=tan∠PQA=
=
=
.
故选B
 解:连接OQ,AQ,过A作AM⊥PQ,如图所示:
解:连接OQ,AQ,过A作AM⊥PQ,如图所示:∵PQ为圆O的切线,
∴OQ⊥PQ,
在Rt△OPQ中,tanP=
| OQ |
| PQ |
| 3 |
| 4 |
设OQ=3k,则PQ=4k,根据勾股定理得:OP=5k,
AP=OP-OA=5k-3k=2k,
∵∠OQP=∠AMP=90°,∠P=∠P,
∴△APM∽△OPQ,
∴
| AM |
| OQ |
| AP |
| OP |
∴AM=
| AP•OQ |
| OP |
| 6 |
| 5 |
在Rt△APM中,AP=2k,AM=
| 6 |
| 5 |
根据勾股定理得:PM=
| AP2-AM2 |
| 8 |
| 5 |
∴MQ=PQ-PM=4k-
| 8 |
| 5 |
| 12 |
| 5 |
∵∠PQA=∠B,
∴tanB=tan∠PQA=
| AM |
| MQ |
| ||
|
| 1 |
| 2 |
故选B
点评:此题考查了切线的性质,锐角三角函数定义,勾股定理,以及相似三角形的判定与性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
 田间有两条平行小路AC、BD,这两条小路分别与一条公路AB在A、B两处相交,并且相交的角度∠1=120°,现在想经过C处修一条水渠,使水渠与公路平行,那么∠2的度数应该是( )
田间有两条平行小路AC、BD,这两条小路分别与一条公路AB在A、B两处相交,并且相交的角度∠1=120°,现在想经过C处修一条水渠,使水渠与公路平行,那么∠2的度数应该是( )| A、120 | B、30 | C、60 | D、80 |
从2,3,4,5这四个数中,任取两个数p和q(p≠q),构成函数y=px-2和y=x+q,若两个函数图象的交点在直线x=2的左侧,则这样的有序数组(p,q)共有( )
| A、10组 | B、6组 | C、5组 | D、4组 |
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 在一条河流的平行两岸边,分别栽有一根标杆A,B,测得线段AB与河岸垂直,并且AB=40米,那么,标杆A到对岸的距离等于
在一条河流的平行两岸边,分别栽有一根标杆A,B,测得线段AB与河岸垂直,并且AB=40米,那么,标杆A到对岸的距离等于 如图,AD是△ABC的中线,E是AC上的一点,且AE:EC=1:3,设BE与AD交于G,则AG:GD=
如图,AD是△ABC的中线,E是AC上的一点,且AE:EC=1:3,设BE与AD交于G,则AG:GD=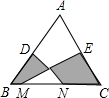 如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为
如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为 ,下列命题,是假命题的个数是( )
,下列命题,是假命题的个数是( )