题目内容
 如图,梯形ABCD中,AB∥CD,AB=AC=AD,若∠BAD=140°,则∠B的度数为( )
如图,梯形ABCD中,AB∥CD,AB=AC=AD,若∠BAD=140°,则∠B的度数为( )| A、60° | B、70° |
| C、75° | D、80° |
考点:梯形
专题:
分析:由已知条件可知△ADC和△ABC都是等腰三角形,设∠DCA=x°,利用平行线的性质和三角形的内角和定理以及等腰三角形的性质列方程求解即可.
解答:解:∵AB=AC=AD,
∴△ADC和△ABC都是等腰三角形,
∴∠D=∠DCA,∠ACB=∠ABC,
设∠DCA=x°,
∵AB∥CD,
∴∠CAB=∠DCA=x°,
∵∠BAD=140°,
∴∠DAC=140°-x°,
∵∠D+∠DAC+∠DCA=180°,
∴140°-x°+x°+x°=180°,
∴x=40°,
∴∠B=
=70°.
故选B.
∴△ADC和△ABC都是等腰三角形,
∴∠D=∠DCA,∠ACB=∠ABC,
设∠DCA=x°,
∵AB∥CD,
∴∠CAB=∠DCA=x°,
∵∠BAD=140°,
∴∠DAC=140°-x°,
∵∠D+∠DAC+∠DCA=180°,
∴140°-x°+x°+x°=180°,
∴x=40°,
∴∠B=
| 180°-40° |
| 2 |
故选B.
点评:本题考查了等腰三角形的性质,平行线的性质以及三角形的内角和定理.此题列方程解题更直接.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 田间有两条平行小路AC、BD,这两条小路分别与一条公路AB在A、B两处相交,并且相交的角度∠1=120°,现在想经过C处修一条水渠,使水渠与公路平行,那么∠2的度数应该是( )
田间有两条平行小路AC、BD,这两条小路分别与一条公路AB在A、B两处相交,并且相交的角度∠1=120°,现在想经过C处修一条水渠,使水渠与公路平行,那么∠2的度数应该是( )| A、120 | B、30 | C、60 | D、80 |
从2,3,4,5这四个数中,任取两个数p和q(p≠q),构成函数y=px-2和y=x+q,若两个函数图象的交点在直线x=2的左侧,则这样的有序数组(p,q)共有( )
| A、10组 | B、6组 | C、5组 | D、4组 |
已知x≠-1,0,1,则
+
+
的值可能是( )
| x-1 |
| |x-1| |
| |x| |
| x |
| x+1 |
| |x+1| |
| A、比3大的数 |
| B、比-3小的数 |
| C、±1,±3 |
| D、比-3大,并且比3小的数 |
下列图形中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
与4的和为0的数是( )
| A、4 | ||
| B、-4 | ||
| C、0 | ||
D、-
|
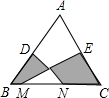 如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为
如图,在△ABC中,AB=AC,D、E分别是AB、AC的中点,M、N为BC上的点,连接DN、EM.若AB=10cm,BC=12cm,MN=6cm,则图中阴影部分的面积为