题目内容
9.如图,在数轴上放置一个长方形块,长方形的长为$\frac{3}{4}$,宽为$\frac{1}{3}$.此时将长方形沿数轴正方向做顺时针的翻动.长方形所在的初始位置如图中实线所示,沿A点(如图所示)做数轴的垂线,在数轴上所对应的数字是1.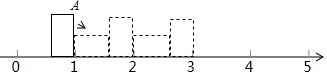
| 翻动次数 | A点在数轴上对应的数字 |
| 1 | 1+$\frac{3}{4}$ |
| 2 | 1+$\frac{3}{4}$+0 |
| 3 | |
| 4 |
(2)第8次翻动长方形块后,A点在数轴上所对应的数字表示是5$\frac{1}{3}$
(3)第101次翻动长方形块后,A点在数轴上所对应的数字表示是55$\frac{11}{12}$.
分析 (1)翻动长方形块后,A点在数轴上所对应的数字表示是:
第1次:1+$\frac{3}{4}$,
第2次:1+$\frac{3}{4}$+0,
第3次:1+$\frac{3}{4}$+0+$\frac{1}{3}$,
(2)第4次:1+$\frac{3}{4}$+0+$\frac{1}{3}$+$\frac{3}{4}$+$\frac{1}{3}$=1+2×($\frac{3}{4}$+$\frac{1}{3}$),
…
第8次:1+4×($\frac{3}{4}$+$\frac{1}{3}$),
发现是4次一循环,加一个周长;做顺时针的翻动时边依次相加:$\frac{3}{4}$,0,$\frac{1}{3}$,$\frac{3}{4}$+$\frac{1}{3}$,
(3)所以第101次翻动,要先计算101÷4=25余1,即翻动了25个长方形的周长还余一次,即1+50×($\frac{3}{4}$+$\frac{1}{3}$)+$\frac{3}{4}$=55$\frac{11}{12}$.
解答 (1)1+$\frac{3}{4}$+$\frac{1}{3}$=$\frac{12+9+4}{12}$=$\frac{25}{12}$,
则第3次翻动长方形块后,A点在数轴上所对应的数字表示是$\frac{25}{12}$,
(2)1+4×($\frac{3}{4}$+$\frac{1}{3}$)=$\frac{16}{3}$=$5\frac{1}{3}$,
则第8次翻动长方形块后,A点在数轴上所对应的数字表示是5$\frac{1}{3}$,
(3)101÷4=25余1,
∴1+50×($\frac{3}{4}$+$\frac{1}{3}$)+$\frac{3}{4}$=55$\frac{11}{12}$,
则第101次翻动长方形块后,A点在数轴上所对应的数字表示是55$\frac{11}{12}$,
故答案为:(1)$\frac{25}{12}$,(2)5$\frac{1}{3}$,(3)55$\frac{11}{12}$.
点评 本题是实数和数轴的问题,也是长方形木块做顺时针翻动的问题,此类题的解题思路为:先依次根据翻动的情况找规律,再进行计算.

| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2010 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
| A. | 6℃ | B. | 7℃ | C. | 8℃ | D. | 57℃ |
 将抛物线在第四象限之间的部分图象记为图象G,如果直线y=k(x+1)-4与图象G有公共点,请结合图象,求直线y=k(x+1)-4与y轴交点的纵坐标t的取值范围.
将抛物线在第四象限之间的部分图象记为图象G,如果直线y=k(x+1)-4与图象G有公共点,请结合图象,求直线y=k(x+1)-4与y轴交点的纵坐标t的取值范围.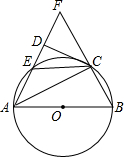 如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,
如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,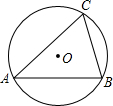 如图,锐角△ABC是⊙O的内接三角形,若AC=17cm,BC=10cm,⊙O的直径是21.25cm,则△ABC的面积是84cm2.
如图,锐角△ABC是⊙O的内接三角形,若AC=17cm,BC=10cm,⊙O的直径是21.25cm,则△ABC的面积是84cm2.