题目内容
6.先化简,再求值:(2x+y)2+(x-y)(x+y)-5x(x-y),其中x=$\sqrt{2}$+1,y=$\sqrt{2}$-1.分析 首先化简(2x+y)2+(x-y)(x+y)-5x(x-y),然后把x=$\sqrt{2}$+1,y=$\sqrt{2}$-1代入化简后的算式,求出算式的值是多少即可.
解答 解:(2x+y)2+(x-y)(x+y)-5x(x-y)
=4x2+4xy+y2+x2-y2-5x2+5xy
=9xy
当x=$\sqrt{2}$+1,y=$\sqrt{2}$-1时,
原式=9($\sqrt{2}$+1)($\sqrt{2}$-1)
=9×(2-1)
=9×1
=9
点评 此题主要考查了整式的混合运算-化简求值问题,要熟练掌握,解答此题的关键是要明确:先按运算顺序把整式化简,再把对应字母的值代入求整式的值.

练习册系列答案
相关题目
17.某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
(说明:成绩80分及以上为生产技能优秀,70--79分为生产技能良好,60--69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
得出结论:a.估计乙部门生产技能优秀的员工人数为240;b.可以推断出甲或乙部门员工的生产技能水平较高,理由为①甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高..(至少从两个不同的角度说明推断的合理性)
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90 75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83 80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:
| 成绩x 人数 部门 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
| 甲 | 0 | 0 | 1 | 11 | 7 | 1 |
| 乙 | 1 | 0 | 0 | 7 | 10 | 2 |
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
| 部门 | 平均数 | 中位数 | 众数 |
| 甲 | 78.3 | 77.5 | 75 |
| 乙 | 78 | 80.5 | 81 |
②甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高.
或①乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
②乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高..(至少从两个不同的角度说明推断的合理性)
14.下列各数中比1大的数是( )
| A. | 2 | B. | 0 | C. | -1 | D. | -3 |
11. 图中立体图形的主视图是( )
图中立体图形的主视图是( )
 图中立体图形的主视图是( )
图中立体图形的主视图是( )| A. |  | B. |  | C. |  | D. |  |
18.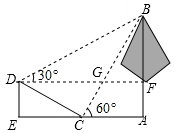 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.
如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.
 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.
如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是( )m.| A. | 20$\sqrt{3}$ | B. | 30 | C. | 30$\sqrt{3}$ | D. | 40 |
4. 如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
 如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )
如图,AB∥CD,AD=CD,∠2=40°,则∠1的度数是( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
 如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE:∠EFB=3:4,∠ABF=40°,那么∠BEF的度数为60°.
如图,AB∥CD,点E在AB上,点F在CD上,如果∠CFE:∠EFB=3:4,∠ABF=40°,那么∠BEF的度数为60°. 如图,点C是AB的中点,AD=CE,CD=BE.
如图,点C是AB的中点,AD=CE,CD=BE.