题目内容
1.某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量减少20千克.(1)如果该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(2)当每千克涨价多少元时,该商场的每天盈利最大?
分析 (1)关键是根据题意列出一元二次方程,然后求出其解,最后根据题意确定其值.
(2)根据题意构建二次函数,利用二次函数的性质求其最值.
解答 解:(1)设每千克应涨价x元,由题意,得
(10+x)(500-20x)=6000,
整理,得 x2-15x+50=0,
解得:x=5或x=10,
∴为了使顾客得到实惠,所以x=5.
(2)设涨价x元时总利润为y,由题意,得
y=(10+x)(500-20x)
y=-20x2+300x+5 000
y=-20(x-7.5)2+6125
∴当x=7.5时,y取得最大值,最大值为6125元.
答:(1)要保证每天盈利6000元,同时又使顾客得到实惠,那么每千克应涨价5元;
(2)若该商场单纯从经济角度看,每千克这种水果涨价7.5元,能使商场获利最多为6125元.
点评 此题考查了二次函数的应用,一元二次方程的应用等知识,解题的关键是学会构建二次函数解决最值问题,学会用转化的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
12. 将矩形ABCD沿AE折叠,D点落在F处,若∠CEF=60°,则∠EAB等于( )
将矩形ABCD沿AE折叠,D点落在F处,若∠CEF=60°,则∠EAB等于( )
 将矩形ABCD沿AE折叠,D点落在F处,若∠CEF=60°,则∠EAB等于( )
将矩形ABCD沿AE折叠,D点落在F处,若∠CEF=60°,则∠EAB等于( )| A. | 72° | B. | 60° | C. | 55° | D. | 54° |
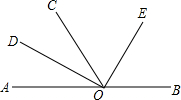 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,请求出∠AOD、∠COE、∠BOC、∠BOE的度数.
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°,请求出∠AOD、∠COE、∠BOC、∠BOE的度数.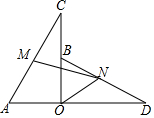 如图,OA=OB,OC=OD,∠AOB=∠COD=90°,M,N分别为AC,BD的中点,连接MN,ON,求证:∠MNO=45°.
如图,OA=OB,OC=OD,∠AOB=∠COD=90°,M,N分别为AC,BD的中点,连接MN,ON,求证:∠MNO=45°.
