题目内容
11.如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律.则第(100)个图形中面积为1的正方形的个数为( )
| A. | 5150 | B. | 5050 | C. | 5100 | D. | 5049 |
分析 由图可知:第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,按此规律,第n个图形中面积为1的正方形有2+3+4+…+n+1=$\frac{n(n+3)}{2}$,进一步求得第(100)个图形中面积为1的正方形的个数即可.
解答 解:第(1)个图形中面积为1的正方形有2个,
第(2)个图形中面积为1的图象有2+3=5个,
第(3)个图形中面积为1的正方形有2+3+4=9个,
…,
按此规律,
第n个图形中面积为1的正方形有2+3+4+…+(n+1)=$\frac{1}{2}$n(n+3)个,
则第(10)个图形中面积为1的正方形的个数为$\frac{1}{2}$×100×103=5150个.
故选A.
点评 此题考查图形的变化规律,利用图形的排列规律,得出数字的运算方法解决问题.

练习册系列答案
相关题目
2.一扇形的半径为24cm,若此扇形围成的圆锥的底面半径为10cm,那么这个扇形的面积是( )
| A. | 120πcm 2 | B. | 240πcm 2 | C. | 260πcm 2 | D. | 480πcm 2 |
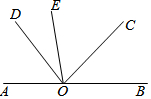 如图,已知,∠AOE=∠COD,且射线OC平分∠EOB,∠EOD=30°.
如图,已知,∠AOE=∠COD,且射线OC平分∠EOB,∠EOD=30°. 在平面直角坐标系中,A(-1,5),B(-2,1),C(-4,3)
在平面直角坐标系中,A(-1,5),B(-2,1),C(-4,3)