题目内容
11．观察下列各式：13=1=$\frac{1}{4}$×12×22
13+23=9=$\frac{1}{4}$×22×32
13+23+33=36=$\frac{1}{4}$×32×42
13+23+33+43=100=$\frac{1}{4}$×42×52
…
回答下面的问题：
（1）猜想13+23+33+…+（n-1）3+n3=$\frac{1}{4}$n2（n+1）2
（2）利用你得到的（1）中的结论，计算13+23+33+…+993+1003的值；
（3）计算：
①213+223+…+993+1003的值；
②23+43+63+…+983+1003的值．
分析 （1）（2）观察已知的等式，发现：等式的左边是连续自然数的立方和，等式的右边是连续自然数的和的平方；由此得出答案即可；
（3）根据（1）中发现的结论，即可求得结论．
解答 解：（1）$\frac{1}{4}$n2（n+1）2；
（2）13+23+33+…+1003=$\frac{1}{4}$×1002×1012=25502500；
（3）①原式=13+23+33+…+993+1003-（13+23+33+43+…203）=$\frac{1}{4}$×1002×1012-$\frac{1}{4}$×202×212=25458400；
②原式=23×（13+23+33++…503=8×$\frac{1}{4}$×502×512=13005000．
点评 此题考查数字的变化规律，找出数字的变化规律，利用规律解决问题．
练习册系列答案
相关题目
如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与图中△ABC相似的是（ ）
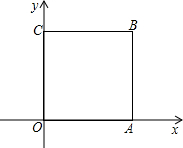如图所示，正方形OABC的顶点为O（0，0），A（1，0），B（1，1），C（0，1）．
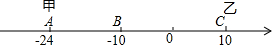已知数轴上有A、B、C三点，分别代表-24，-10，10，两只电子蚂蚁甲、乙分别从A、C两点同时相向而行，甲的速度为4个单位/秒，乙的速度为6个单位/秒．