题目内容
3.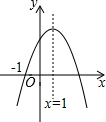 一次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x>3,y>0.正确的个数是( )
一次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①c<0;②b2-4ac>0;③a+2b=0;④当x>3,y>0.正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据抛物线与y轴的交点在x轴上方得c>0,则可对①进行判断;根据抛物线与x轴有两个交点可对②进行判断;根据抛物线的对称轴为直线x=1,则b=-2a,则可对③进行判断;抛物线与x轴正半轴另一交点坐标为3,所以当-1<x<3时,y>0,x<-1时,y<0,于是可对④进行判断.
解答 解:∵抛物线与y轴的交点在x轴上方,
∴c>0,所以①错误;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,所以②正确;
∵抛物线开口向下,
∴a<0;
∵抛物线对称轴为直线x=-$\frac{b}{2a}$=1,
∴b>0,b=-2a,
∴a+2b=a-4a=-3a>0,所以③错误;
∵对称轴为直线x=1,
∴抛物线与x轴正半轴的交点坐标为3,
∴当x=3时,y=0,
∴-1<x<3时,y>0,
当x<-1时,y<0,
所以④错误.
故选A.
点评 本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标;当b2-4ac>0,抛物线与x轴有两个交点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.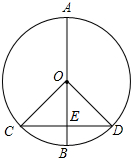 如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
 如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )
如图,AB是⊙O的直径,CD是弦,CD⊥AB于E,则下列结论错误的是( )| A. | ∠AOC=∠AOD | B. | BE=OE | C. | CE=DE | D. | AC=AD |
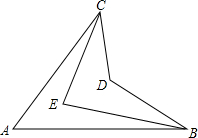 如图,若∠ACE=$\frac{1}{3}$∠ACD,∠ABE=$\frac{1}{3}$∠ABD,猜想∠A,∠CEB和∠CDB之间的数量关系为2∠A+∠CDB=3∠CEB.(写出结论,不必证明)
如图,若∠ACE=$\frac{1}{3}$∠ACD,∠ABE=$\frac{1}{3}$∠ABD,猜想∠A,∠CEB和∠CDB之间的数量关系为2∠A+∠CDB=3∠CEB.(写出结论,不必证明) 如图是由六块积木搭成,这几块积木都是相同的正方体,请画出这个图形的三视图:
如图是由六块积木搭成,这几块积木都是相同的正方体,请画出这个图形的三视图: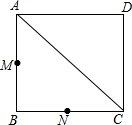 如图,四边形ABCD为正方形,M,N分别是AB,BC边的中点,请在对角线AC上找一点P,使PM+PN的值最小(不写作法,保留作图痕迹).
如图,四边形ABCD为正方形,M,N分别是AB,BC边的中点,请在对角线AC上找一点P,使PM+PN的值最小(不写作法,保留作图痕迹). 小刚要从A地赶往C地去参加科技夏令营,他拿出一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A的南偏西55°,在B地的北偏西70°,如图所示.
小刚要从A地赶往C地去参加科技夏令营,他拿出一张地图,图上有A、B、C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A的南偏西55°,在B地的北偏西70°,如图所示.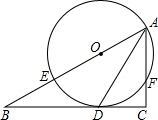 如图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上
如图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上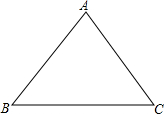 请思考如何利用位似变换的思想,在如图的三角形中作一个等边三角形,使它的三个顶点分别在已知三角形的边上,并且等边三角形的一边与BC平行,即:已知△ABC,求作等边△DEF,使它的三个顶点分别在△ABC的边上,且EF∥BC.
请思考如何利用位似变换的思想,在如图的三角形中作一个等边三角形,使它的三个顶点分别在已知三角形的边上,并且等边三角形的一边与BC平行,即:已知△ABC,求作等边△DEF,使它的三个顶点分别在△ABC的边上,且EF∥BC.