题目内容
2．
如图，在Rt△ABC中，∠C=90°，∠CAB=60°，AD平分∠CAB，点D到AB的距离DE是3cm，求BC．
分析 根据角平分线上的点到角的两边距离相等可得CD=DE，再求出∠CAD=∠BAD=∠B=30°，再根据直角三角形30°所对的直角边等于斜边的一半可得AD=2CD，根据等角对等边可得BD=AD，然后利用BC=CD+BD计算即可得解．
解答 解：∵AD平分∠CAB，∠C=90°，
∴CD=DE=3cm．
∵∠CAB=60°，AD平分∠CAB，
∴∠CAD=∠BAD=∠B=30°，
∴AD=2CD=2×3=6cm，BD=AD=6cm．
∴BC=CD+BD=3+6=9cm．
点评 本题考查了角平分线上的点到角的两边距离相等的性质，直角三角形30°所对的直角边等于斜边的一半的性质，等角对等边的性质，熟记各性质是解题的关键．
练习册系列答案
相关题目
13．
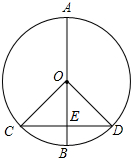如图，AB是⊙O的直径，CD是弦，CD⊥AB于E，则下列结论错误的是（ ）
如图，AB是⊙O的直径，CD是弦，CD⊥AB于E，则下列结论错误的是（ ）| A． | ∠AOC=∠AOD | B． | BE=OE | C． | CE=DE | D． | AC=AD |
将连续的偶数2，4，6，8，…排列成如图所示的数表，设中间的数为a，用代数式表示“+”字框内5个数之和为5a．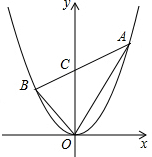
如图，过点C（0，3）的直线交抛物线y=x2于A、B两点，若S△AOB=6，求点A、B的坐标．
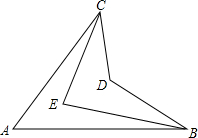如图，若∠ACE=$\frac{1}{3}$∠ACD，∠ABE=$\frac{1}{3}$∠ABD，猜想∠A，∠CEB和∠CDB之间的数量关系为2∠A+∠CDB=3∠CEB．（写出结论，不必证明）
如图是由六块积木搭成，这几块积木都是相同的正方体，请画出这个图形的三视图：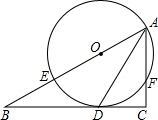
如图，在Rt△ABC中，∠C=90°，AC=12，BC=16，∠BAC的平分线交BC于D，经过A、D的⊙O交AB于E，并且点O在AB上