题目内容
12.观察规律:$\begin{array}{l}\frac{1}{{\sqrt{2}+1}}=\frac{{\sqrt{2}-1}}{{({\sqrt{2}+1})({\sqrt{2}-1})}}=\frac{{\sqrt{2}-1}}{2-1}=\sqrt{2}-1\end{array}\begin{array}{l}$
$\frac{1}{{\sqrt{3}+\sqrt{2}}}=\frac{{\sqrt{3}-\sqrt{2}}}{{({\sqrt{3}+\sqrt{2}})({\sqrt{3}-\sqrt{2}})}}=\frac{{\sqrt{3}-\sqrt{2}}}{3-2}=\sqrt{3}-\sqrt{2}\end{array}$
同理可得:$\begin{array}{l}\frac{1}{{\sqrt{4}+\sqrt{3}}}=\sqrt{4}-\sqrt{3}\end{array}$
依照上述规律,则:$\frac{1}{{\sqrt{11}+\sqrt{10}}}$=$\sqrt{11}$-$\sqrt{10}$; $\frac{1}{{\sqrt{n+1}+\sqrt{n}}}$=$\sqrt{n+1}$-$\sqrt{n}$(n≥1的整数);
$({\frac{1}{{\sqrt{2}+1}}+\frac{1}{{\sqrt{3}+\sqrt{2}}}+\frac{1}{{\sqrt{4}+\sqrt{3}}}+…+\frac{1}{{\sqrt{2016}+\sqrt{2015}}}})({\sqrt{2016}+1})$=2015.
分析 仿照上述计算过程将原式变形,化简即可得到结果;原式括号中分母有理化后,利用平方差公式计算即可得到结果.
解答 解:$\frac{1}{\sqrt{11}+\sqrt{10}}$=$\frac{\sqrt{11}-\sqrt{10}}{(\sqrt{11}+\sqrt{10})(\sqrt{11}-\sqrt{10})}$=$\sqrt{11}$-$\sqrt{10}$,$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$,
原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2016}$-$\sqrt{2015}$)($\sqrt{2016}$+1)=($\sqrt{2016}$-1)($\sqrt{2016}$+1)=2016-1=2015,
故答案为:$\sqrt{11}$-$\sqrt{10}$;$\sqrt{n+1}$-$\sqrt{n}$;2015
点评 此题考查了分母有理化,二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
相关题目
13. 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )| A. | 0,1,-2 | B. | 1,0,-2 | C. | -2,0,1 | D. | 0,-2,1 |
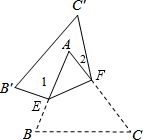 如图,把△ABC沿EF对折,折叠后的图形如图所示.若∠A=60°,∠1=96°,则∠2的度数为24°.
如图,把△ABC沿EF对折,折叠后的图形如图所示.若∠A=60°,∠1=96°,则∠2的度数为24°.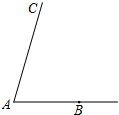 如图,已知∠CAB,用直尺和圆规作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射线BD与射线AC相交于点D.(不写画法,保留作图痕迹)
如图,已知∠CAB,用直尺和圆规作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射线BD与射线AC相交于点D.(不写画法,保留作图痕迹) 已知如图,AC、BD相交于点O,且被点O互相平分,求证:
已知如图,AC、BD相交于点O,且被点O互相平分,求证: