题目内容
6.如图一组有规律的正多边形,各正多边形中的阴影部分面积均为a,按此规律,则第n个正多边形的面积为$\frac{n+1}{2}$a.
分析 设出正多边形的边长,根据正多边形与圆的关系,分别求出正四边形、正六边形和正八边形的面积,找出规律,得到答案.
解答 解:第一个:正多边形的面积等于a;
第二个:如图作AE⊥BD于E,
设正六边形的边长为2,
∵正六边形的一个内角为120°,
∴∠ABE=30°,
则AE=1,BE=$\sqrt{3}$,
△ABD的面积为:$\frac{1}{2}$×2$\sqrt{3}$×1=$\sqrt{3}$,
a=2×2$\sqrt{3}$=4$\sqrt{3}$,
∴正六边形的面积为:$\frac{3}{2}$a,
第三个:如图,
∵正八边形的一个内角为135°,
∴∠ABD=45°,
设正八边形的边长为2,
则BD=AD=$\sqrt{2}$,△ABD的面积为1,
四边形ABEF的面积为1+2$\sqrt{2}$+1=2$\sqrt{2}$+2,
a=2×(2$\sqrt{2}$+2)=4$\sqrt{2}$+4,
∴正八边形的面积为2a,
通过计算可以看出:第n个正多边形的面积为$\frac{n+1}{2}$a.
点评 本题考查的是正多边形与圆的关系,求出正多边形的一个内角,设出边长,根据特殊角的性质和勾股定理表示出有关的边长,求出正多边形的面积,根据计算结果找出规律是解题的关键.

练习册系列答案
相关题目
17.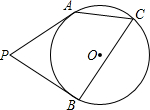 如图,PA、PB与⊙O相切于A、B两点,C为优弧$\widehat{AB}$上一点,若tan∠ACB=2,则sin∠APB的值为( )
如图,PA、PB与⊙O相切于A、B两点,C为优弧$\widehat{AB}$上一点,若tan∠ACB=2,则sin∠APB的值为( )
 如图,PA、PB与⊙O相切于A、B两点,C为优弧$\widehat{AB}$上一点,若tan∠ACB=2,则sin∠APB的值为( )
如图,PA、PB与⊙O相切于A、B两点,C为优弧$\widehat{AB}$上一点,若tan∠ACB=2,则sin∠APB的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{12}$ | D. | $\frac{\sqrt{5}}{5}$ |
1.直线y=kx(k>0)与双曲线y=$\frac{2}{x}$交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则(x1-x2)(y1-y2)的值为( )
| A. | -4 | B. | 0 | C. | 4 | D. | 8 |
11. 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
 实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )
实数a,b,c在数轴上对应的点如图所示,则下列式子中正确的是( )| A. | ac>bc | B. | |a-b|=a-b | C. | -a-c>-b-c | D. | -a<-b<c |
15. 由5个相同的小正方体搭成的物体的俯视图如图所示,则这个物体的搭法有( )
由5个相同的小正方体搭成的物体的俯视图如图所示,则这个物体的搭法有( )
 由5个相同的小正方体搭成的物体的俯视图如图所示,则这个物体的搭法有( )
由5个相同的小正方体搭成的物体的俯视图如图所示,则这个物体的搭法有( )| A. | 4种 | B. | 3种 | C. | 2种 | D. | 1种 |