题目内容
20.已知,Rt△ABC中,∠BAC=90°,点D是直线AC上的动点,过点D作BC⊥DE交直线BC于点F,连接EC,且EC=ED,DC=2AB,将线段DE绕点E旋转90°得到线段GE,连结BG.(1)如图1,当点D在线段AC上时,证明:四边形BCEG为菱形:
(2)如图2.当点D在线段AC的延长线上时,(1)的结论:四边形BCEG为菱形是否依然成立,若成立,请给出证明;若不成立,请说明理由.
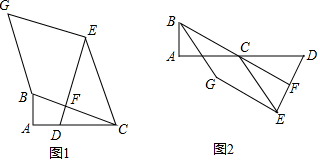
分析 (1)过E作EH⊥CD于H,根据等腰三角形的性质得到DH=$\frac{1}{2}$CD,等量代换得到AB=DH,根据余角的性质得到∠ACB=∠DEH,根据全等三角形的性质得到BC=DE=CE,根据旋转的性质得到∠GED=90°,GE=DE,即可得到结论.
(2)过E作EH⊥CD于H,根据等腰三角形的性质得到DH=$\frac{1}{2}$CD,等量代换得到AB=DH,根据余角的性质得到∠ACB=∠DEH,根据全等三角形的性质得到BC=DE=CE,根据旋转的性质得到∠GED=90°,GE=DE,即可得到结论.
解答 解:(1)过E作EH⊥CD于H,
∵EC=ED,
∴DH=$\frac{1}{2}$CD,
∵DC=2AB,
∴AB=DH,
∵BC⊥DE,
∴∠DEH+∠EDH=∠ACB+∠CDF=90°,
∴∠ACB=∠DEH,
在△ABC与△HDE中,
$\left\{\begin{array}{l}{∠ACB=∠DEH}\\{∠A=∠DHE}\\{AB=DH}\end{array}\right.$,
∴△ABC≌△HDE,
∴BC=DE=CE,
∵将线段DE绕点E旋转90°得到线段GE,
∴∠GED=90°,GE=DE,
∴GE∥BC,GE=BC,
∴四边形BCEG是平行四边形,
∵BC=CE,
∴四边形BCEG为菱形;
(2)过E作EH⊥CD于H,
∵EC=ED,
∴DH=$\frac{1}{2}$CD,
∵DC=2AB,
∴AB=DH,
∵BC⊥DE,
∴∠DEH+∠EDH=∠DCF+∠CDF=90°,
∴∠ACB=∠DEH=∠DCF,
在△ABC与△HDE中,
$\left\{\begin{array}{l}{∠ACB=∠DEH}\\{∠A=∠DHE}\\{AB=DH}\end{array}\right.$,
∴△ABC≌△HDE,
∴BC=DE=CE,
∵将线段DE绕点E旋转90°得到线段GE,
∴∠GED=90°,GE=DE,
∴GE∥BC,GE=BC,
∴四边形BCEG是平行四边形,
∵BC=CE,
∴四边形BCEG为菱形.
点评 本题考查了旋转的性质,菱形的判定和性质,全等三角形的判定和性质,等腰三角形的性质,熟练掌握菱形的判定和性质定理是解题的关键.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 如图,在等腰三角形ABC中,D是BC边上的一点,DE⊥AB,DE⊥AC,点E、F分别是垂足,若DE+DF=2$\sqrt{2}$,△ABC的面积为$\frac{8\sqrt{6}}{5}$,求AB的长.
如图,在等腰三角形ABC中,D是BC边上的一点,DE⊥AB,DE⊥AC,点E、F分别是垂足,若DE+DF=2$\sqrt{2}$,△ABC的面积为$\frac{8\sqrt{6}}{5}$,求AB的长.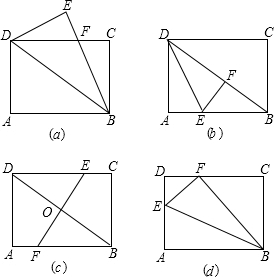
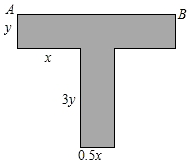 某种T型零件尺寸如图所示(左右宽度相同),求:
某种T型零件尺寸如图所示(左右宽度相同),求: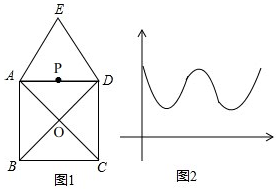
 如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点.
如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点.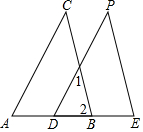 如图,∠1=∠C,∠2=∠E,指出图中哪些直线是平行的,并说出理由.
如图,∠1=∠C,∠2=∠E,指出图中哪些直线是平行的,并说出理由.