题目内容
18.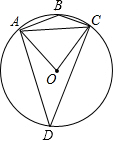 如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )
如图,⊙O是四边形ABCD的外接圆,连接AC,OA,OC,若∠ABC:∠ACO=13:4,则∠ADC的度数为( )| A. | 30° | B. | 50° | C. | 40° | D. | 45° |
分析 设∠ABC=13x°,∠ACO=4x°,求出∠AOC,求出∠ADC,根据圆内接四边形得出方程,求出x即可.
解答 解:∵∠ABC:∠ACO=13:4,
∴设∠ABC=13x°,∠ACO=4x°,
∵OA=OC,
∴∠OAC=∠ACO=4x°,
∴∠AOC=180°-∠OAC-∠ACO=180°-8x°,
∴由圆周角定理得:∠ADC=$\frac{1}{2}$∠AOC=90°-4x°,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴13x+90-4x=180,
解得:x=10,
∴∠ADC=90°-4×10°=50°,
故选B.
点评 本题考查了圆周角定理和圆内接四边形,能根据定理得出方程是解此题的关键.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | 3a-1=$\frac{1}{3a}$ | B. | a-2+2a-1=2a-3 | C. | (-a)-3a2=-a-6 | D. | (-a)-3÷(-a-4)=a |
9.在3,0,π,-4这四个数中,最大的是( )
| A. | 3 | B. | 0 | C. | π | D. | -4 |
6.如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,以此类推,依此类推,图10中有10个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S10,则S1+S2+S3+…+S10=( )
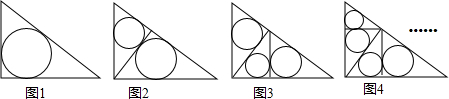

| A. | 4π | B. | 3π | C. | 2π | D. | π |
13.下列运算正确的是( )
| A. | 8a2-4a=4a | B. | (-a3b)2=a6b2 | C. | a-2+a2=a0 | D. | a2•4a4=4a8 |
10.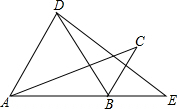 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )| A. | ∠ABD=∠E | B. | ∠CBE=∠C | C. | AD∥BC | D. | AD=BC |
7.数据6,5,7.5,8.6,7,6的众数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
8.5的相反数是( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | $-\frac{1}{5}$ | D. | -5 |
 已知抛物线C1:y=ax2-4ax-5(a>0).
已知抛物线C1:y=ax2-4ax-5(a>0).