题目内容
已知A(1,1),B(3,5),点P是x轴上一动点,且PA+PB值最小,则P点坐标为 .
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:根据题意画出图形,作出A点关于y轴的对称点A′,连接A′B,与y轴相交于P点,由两点之间线段最短的特点可知P点即为所求,设P点坐标为(0,a),再用待定系数法求出过A′B的一次函数关系式,把P点的坐标代入即可求解.
解答: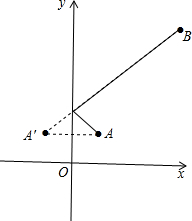 解:如图所示,
解:如图所示,
作出A点关于y轴的对称点A′,则A′点的坐标为(-1,1),连接A′B,
设过A′B的直线解析式为y=kx+b(k≠0),
把A′(-1,1)、B(3,5)代入得
,
解得k=1,b=2,
故此直线的解析式为y=x+2,
设P(0,a),则a=2,即P点坐标为(0,2).
故答案为(0,2).
 解:如图所示,
解:如图所示,作出A点关于y轴的对称点A′,则A′点的坐标为(-1,1),连接A′B,
设过A′B的直线解析式为y=kx+b(k≠0),
把A′(-1,1)、B(3,5)代入得
|
解得k=1,b=2,
故此直线的解析式为y=x+2,
设P(0,a),则a=2,即P点坐标为(0,2).
故答案为(0,2).
点评:本题考查的是最短路线问题及用待定系数法求一次函数的解析式,根据轴对称的性质作出A′点并求出其坐标是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
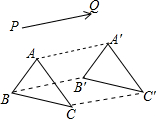 如图,△ABC沿PQ的方向平移到△A′B′C′的位置,AA′、BB′、CC′分别是对应点的连线,请问图中共有多少个平行四边形( )
如图,△ABC沿PQ的方向平移到△A′B′C′的位置,AA′、BB′、CC′分别是对应点的连线,请问图中共有多少个平行四边形( )| A、0个 | B、1个 | C、2个 | D、3个 |
 如图,已知直线y=
如图,已知直线y=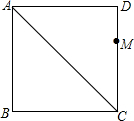 作图题:线段AC是正方形ABCD的对角线,点M是边CD上的一定点(不与D、C重合),请在对角线AC上取一点P,使得△PDM的周长值最小,并作简要说明.
作图题:线段AC是正方形ABCD的对角线,点M是边CD上的一定点(不与D、C重合),请在对角线AC上取一点P,使得△PDM的周长值最小,并作简要说明. 如图是李佳阳和蝴蝶夫人在做数学题时遇到的问题:已知矩形ABCD的顶点A在坐标原点,AB,AD分别在x轴,y轴的正半轴上,点B的坐标为(1,0),点D的坐标为(0,
如图是李佳阳和蝴蝶夫人在做数学题时遇到的问题:已知矩形ABCD的顶点A在坐标原点,AB,AD分别在x轴,y轴的正半轴上,点B的坐标为(1,0),点D的坐标为(0,
 如图,MN是⊙O的直径,MN=6,点B是ON上一动点,四边形ABCD和AEFG都是正方形,其中G、A在MN上,C、F在圆上,则正方形ABCD与正方形AEFG的面积和为( )
如图,MN是⊙O的直径,MN=6,点B是ON上一动点,四边形ABCD和AEFG都是正方形,其中G、A在MN上,C、F在圆上,则正方形ABCD与正方形AEFG的面积和为( )