题目内容
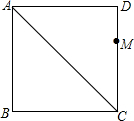作图题：线段AC是正方形ABCD的对角线，点M是边CD上的一定点（不与D、C重合），请在对角线AC上取一点P，使得△PDM的周长值最小，并作简要说明．考点：轴对称-最短路线问题
专题：作图题
分析：连接BM，交AC于P，P即为所求．
解答：解：连接BM，交AC于P，P即为所求；由于四边形ABCD是正方形，所以B、D关于AC对称，所以PB=PD，所以PD+PM=BM最小，故此时△PDM的周长值最小；
点评：本题考查了正方形的性质，轴对称-最短路线问题，确定P的位置是本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知一个四棱锥的正视图和俯视图如图所示，其中a+b=10，则该四棱锥体积的最大值为（ ）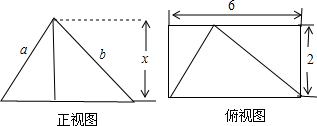
A、8
| ||
B、24
| ||
| C、16 | ||
| D、48 |
数a，b，c在数轴上的对应点如图所示，且表示数a的点与表示数b的点到原点的距离相等．
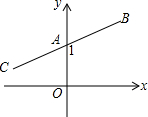如图，点A，点B的坐标分别是（0，1），（a，b），将线段AB绕A旋转180°后得到线段AC，则点C的坐标为（ ）| A、（-a，-b+1） |
| B、（-a，-b-1） |
| C、（-a，-b+2） |
| D、（-a，-b-2） |