题目内容
19．先化简下式，再求值：4x2y-[6xy2-2（4xy2-2）-x2y]+1，其中x=-$\frac{1}{2}$，y=4．分析 根据去括号、合并同类项，可化简整式，根据代数式求值，可得答案．
解答 解：原式=4x2y-[6xy2-8xy2+4-x2y]+1
=4x2y+2xy2-4+x2y+1
=5x2y+2xy2-3，
当x=-$\frac{1}{2}$，y=4时，原式=5×（-$\frac{1}{2}$）2×4+2×（-$\frac{1}{2}$）×42-3
=5+16-3
=18．
点评 本题考查了整式的化简求值，去括号是解题关键，括号前是正数去括号不变号，括号前是负数去括号全变号，注意先去小括号再去中括号．
练习册系列答案
阅读快车系列答案
相关题目
9．
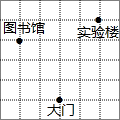如图所示，每个小方格的边长都为1，在直角坐标系中，如果图书馆的横坐标与实验楼的横坐标互为相反数，大门的纵坐标与实验搂的纵图坐标互为相反数，则图书馆的位置是（ ）
如图所示，每个小方格的边长都为1，在直角坐标系中，如果图书馆的横坐标与实验楼的横坐标互为相反数，大门的纵坐标与实验搂的纵图坐标互为相反数，则图书馆的位置是（ ）| A． | （1，5） | B． | （-2，3） | C． | （-2，-1） | D． | （-2，1） |
7．若-$\frac{3}{x}$＞-$\frac{2}{x}$，则x的取值范围为（ ）
| A． | x＞0 | B． | x＜0 | C． | x是整数 | D． | -1＜x＜0 |
14．下列变形中正确的是（ ）
| A． | 9-x2+2xy-y2=9-（-x2-2xy+y2） | B． | 9-x2+2xy-y2=9-（x2-2xy-y2） | ||
| C． | 9-x2+2xy-y2=9-（x2-2xy+y2） | D． | 9-x2+2xy-y2=9+（x2-2xy+y2） |
11．根据下表，回答下列问题．
（1）278.89的平方根是多少？
（2）$\sqrt{259.21}$≈16.1．
（3）$\sqrt{280}$在表中哪两个相邻的数之间？为什么？
| x | 16.0 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 | 16.9 | 17.0 |
| x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 275.56 | 278.89 | 282.24 | 285.61 | 289 |
（2）$\sqrt{259.21}$≈16.1．
（3）$\sqrt{280}$在表中哪两个相邻的数之间？为什么？
9．式子4×25×（$\frac{1}{2}$-$\frac{3}{10}$+$\frac{2}{5}$）=100（$\frac{1}{2}$-$\frac{3}{10}$+$\frac{2}{5}$）=50-30+40中用的运算律是（ ）
| A． | 乘法交换律及乘法结合律 | B． | 乘法交换律及分配律 | ||
| C． | 乘法结合律及分配律 | D． | 分配律及加法结合律 |