题目内容
阅读再解答:
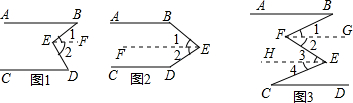
如图1,AB∥CD,试说明:∠B+∠D=∠BED.
可以考虑把∠BED变成两个角的和.过E点引一条直线EF∥AB,则有∠B=∠1,再设法证明∠D=∠2,需证EF∥CD,这可通过已知AB∥CD和EF∥AB得到.
(1)已知:如图2,AB∥CD,则∠BED与∠B、∠D的关系是 ;
(2)已知:如图3,AB∥CD,∠ABF=∠DCE.∠BFE与∠FEC的关系是 .
(3)请你在图2和3中任选一个加以证明.
如图1,AB∥CD,试说明:∠B+∠D=∠BED.
可以考虑把∠BED变成两个角的和.过E点引一条直线EF∥AB,则有∠B=∠1,再设法证明∠D=∠2,需证EF∥CD,这可通过已知AB∥CD和EF∥AB得到.
(1)已知:如图2,AB∥CD,则∠BED与∠B、∠D的关系是
(2)已知:如图3,AB∥CD,∠ABF=∠DCE.∠BFE与∠FEC的关系是
(3)请你在图2和3中任选一个加以证明.

考点:平行线的性质
专题:
分析:(1)作EF∥AB,则EF∥AB∥CD,根据两直线平行,内错角相等即可证得∠B+∠D=360°-∠BED;
(2)作EG∥CD,根据(1)的结论,以及平行线的性质可以证得∠FEC=∠BFE;
(3)证明(1)(2)结论即可.
(2)作EG∥CD,根据(1)的结论,以及平行线的性质可以证得∠FEC=∠BFE;
(3)证明(1)(2)结论即可.
解答:解:(1)证明:作EF∥AB,则EF∥AB∥CD,
∴∠1=180°-∠B,∠2=180°-∠D,
∴∠1+∠2=360°-(∠B+∠D),
即∠B+∠D=360°-∠BED,
故答案为:∠B+∠D=360°-∠BED;
(2)∠BFE=∠FEC,
证明:作FG∥AB,EH∥CD.
根据(1)可以得到∠BFE=∠B+∠3,
∵EH∥CD,
∴∠4=∠C,
又∵∠FEC=∠3+∠4,∠ABF=∠DCE,
∴∠FEC=∠BFE,
故答案为:∠BFE=∠FEC.
(3)已证.
∴∠1=180°-∠B,∠2=180°-∠D,
∴∠1+∠2=360°-(∠B+∠D),
即∠B+∠D=360°-∠BED,
故答案为:∠B+∠D=360°-∠BED;
(2)∠BFE=∠FEC,
证明:作FG∥AB,EH∥CD.
根据(1)可以得到∠BFE=∠B+∠3,
∵EH∥CD,
∴∠4=∠C,
又∵∠FEC=∠3+∠4,∠ABF=∠DCE,
∴∠FEC=∠BFE,
故答案为:∠BFE=∠FEC.
(3)已证.
点评:本题考查了平行线的性质,正确作出辅助线是关键,注意掌握平行线的性质:两直线平行,内错角相等.

练习册系列答案
相关题目
 如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.求证:EC=FA.
如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.求证:EC=FA.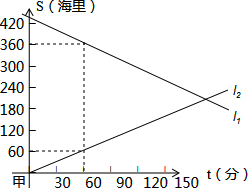 A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船的s与t的关系.
A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船的s与t的关系.  已知四边形ABCD(如图),请在所给的方格纸(图中小正方形的边长为1个单位)内,把四边形ABCD先向右平移6个单位,再向下平移1个单位得到四边形A′B′C′D′.
已知四边形ABCD(如图),请在所给的方格纸(图中小正方形的边长为1个单位)内,把四边形ABCD先向右平移6个单位,再向下平移1个单位得到四边形A′B′C′D′.