题目内容
 如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.求证:EC=FA.
如图,在矩形ABCD中,E、F分别是边AB、CD的中点,连接AF,CE.求证:EC=FA.考点:平行四边形的判定与性质,矩形的性质
专题:证明题
分析:由在矩形ABCD中,E、F分别是边AB、CD的中点,易证得AE∥CF,AE=CF,即可得四边形AECF是平行四边形,继而证得结论.
解答:证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∵E、F分别是边AB、CD的中点,
∴AE=
AB,CF=
CD,
∴AE=CF,
∴四边形AECF是平行四边形,
∴EC=FA.
∴AB∥CD,AB=CD,
∵E、F分别是边AB、CD的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=CF,
∴四边形AECF是平行四边形,
∴EC=FA.
点评:此题考查了平行四边形的判定与性质以及矩形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 尺规作图题.光线从C处射向镜面AB上的点O处,请画出光线经镜面反射后的光线.(保留痕迹不写作法)
尺规作图题.光线从C处射向镜面AB上的点O处,请画出光线经镜面反射后的光线.(保留痕迹不写作法)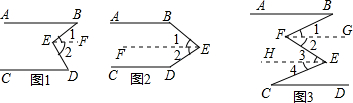
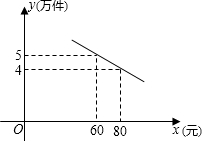 某商场销售一种市场需求较大的健身器材,已知每件产品的进价为40元,每年销售该种产品的总费用(不含进货费用)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元/件)之间存在着如图所示的一次函数关系.若商场希望该种产品一年的销售利润为40万元,请你为商场定一个销售单价.(年销售利润=年销售额-年销售产品进货总费用-年销售总费用)
某商场销售一种市场需求较大的健身器材,已知每件产品的进价为40元,每年销售该种产品的总费用(不含进货费用)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元/件)之间存在着如图所示的一次函数关系.若商场希望该种产品一年的销售利润为40万元,请你为商场定一个销售单价.(年销售利润=年销售额-年销售产品进货总费用-年销售总费用)