题目内容
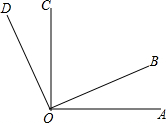 如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.
如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.(1)2∠BOC是哪个角?
(2)
| 1 |
| 2 |
(3)∠AOB+∠BOC等于哪个角?
(4)求∠AOB,∠AOB,∠BOD的度数.
考点:角的计算
专题:
分析:(1)根据角平分线的定义和性质即可解题;
(2)根据角平分线的定义和性质即可解题;
(3)根据角的相加即可解题;
(4)根据∠AOD=120°,∠AOC=75°可以求得∠COD的值,即可解题.
(2)根据角平分线的定义和性质即可解题;
(3)根据角的相加即可解题;
(4)根据∠AOD=120°,∠AOC=75°可以求得∠COD的值,即可解题.
解答:解:(1)∵∠DOC=∠COB,
∴2∠BOC=∠DOC+∠COB=∠BOD;
(2)∵∠DOC+∠COB=∠BOD,∠DOC=∠COB,
∴
∠BOD=∠BOC=∠COD;
(3)从图中可以看出∠AOB+∠BOC=∠AOC;
(4)∵∠AOD=120°,∠AOC=75°,
∴∠COD=120°-75°=45°,
∴∠BOC=∠COD=45°,
∠AOB=∠AOC-∠BOC=30°.
∴2∠BOC=∠DOC+∠COB=∠BOD;
(2)∵∠DOC+∠COB=∠BOD,∠DOC=∠COB,
∴
| 1 |
| 2 |
(3)从图中可以看出∠AOB+∠BOC=∠AOC;
(4)∵∠AOD=120°,∠AOC=75°,
∴∠COD=120°-75°=45°,
∴∠BOC=∠COD=45°,
∠AOB=∠AOC-∠BOC=30°.
点评:本题考查了角的计算,考查了角平分线的性质和定义,本题中求得∠COD的值是解题的关键.

练习册系列答案
相关题目
 如图,已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形ADBC的周长为
如图,已知AB垂直平分CD,AC=6cm,BD=4cm,则四边形ADBC的周长为 如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为5m,则DE的长为
如图是我省某地一座抛物线形拱桥,桥拱在竖直平面内,与水平桥面相交于A,B两点,桥拱最高点C到AB的距离为9m,AB=36m,D,E为桥拱底部的两点,且DE∥AB,点E到直线AB的距离为5m,则DE的长为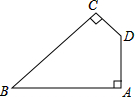 如图,四边形ABCD中,∠A=∠BCD=90°,∠ABC=45°,AD=1,AB=4,求四边形ABCD的面积.
如图,四边形ABCD中,∠A=∠BCD=90°,∠ABC=45°,AD=1,AB=4,求四边形ABCD的面积. 如图,直线y=-
如图,直线y=-