题目内容
已知等腰△ABC的腰长为2,底角为75°,则底边BC的长度为 .
考点:勾股定理,含30度角的直角三角形
专题:
分析:作出图形,过点B作BE⊥AC于E,根据等腰三角形两底角相等求出顶角∠A=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得BE=
AB,再利用勾股定理列式求出AE,然后求出CE,再利用勾股定理列式计算即可得解.
| 1 |
| 2 |
解答: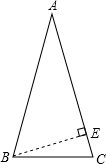 解:如图,过点B作BE⊥AC于E,
解:如图,过点B作BE⊥AC于E,
∵底角为75°,
∴顶角∠A=180°-2×75°=30°,
∴BE=
AB=
×2=1,
在Rt△ABE中,由勾股定理得,AE=
=
=
,
所以,CE=AC-AE=2-
,
在Rt△BCE中,BC=
=
=
=
(
-1)=
-
.
故答案为:
-
.
 解:如图,过点B作BE⊥AC于E,
解:如图,过点B作BE⊥AC于E,∵底角为75°,
∴顶角∠A=180°-2×75°=30°,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ABE中,由勾股定理得,AE=
| AB2-BE2 |
| 22-12 |
| 3 |
所以,CE=AC-AE=2-
| 3 |
在Rt△BCE中,BC=
| BE2+CE2 |
12+(2-
|
2(4-2
|
| 2 |
| 3 |
| 6 |
| 2 |
故答案为:
| 6 |
| 2 |
点评:本题考查了勾股定理,直角三角形30°角所对的直角边等于斜边的一半的性质,勾股定理,作辅助线构造出直角三角形是解题的关键,难点在于被开方数的开方.

练习册系列答案
相关题目
关于x的一元二次方程(a-1)x2-x+a2-1=0的一个根是0,则a的值为( )
| A、1或-1 | ||
| B、-1 | ||
| C、1 | ||
D、
|
在△ABC中,∠A=39°,∠B=41°,则∠C的度数为( )
| A、70° | B、80° |
| C、90° | D、100° |
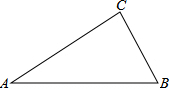 如图是一块直角三角形板材,其中,∠C=90°,AC=8cm,BC=6cm,请问:如何从这块板材上裁剪下一块面积最大的正方形?请画出你的设计图,并求出这块正方形的边长.
如图是一块直角三角形板材,其中,∠C=90°,AC=8cm,BC=6cm,请问:如何从这块板材上裁剪下一块面积最大的正方形?请画出你的设计图,并求出这块正方形的边长. 如图,已知直线AE、CD相交于点O,且∠AOB=90°,∠BOC=28°,求∠DOE、∠AOD的度数.
如图,已知直线AE、CD相交于点O,且∠AOB=90°,∠BOC=28°,求∠DOE、∠AOD的度数.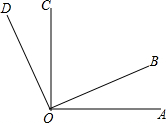 如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°.
如图,∠AOD=120°,∠DOC=∠COB,∠AOC=75°. 如图,已知△ABD∽△ACE.求证:△ABC∽△ADE.
如图,已知△ABD∽△ACE.求证:△ABC∽△ADE.